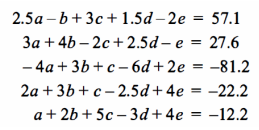1 - چک کردن همگرایی و واگرایی یک سری نامتناهی.(توضیح: در ابتدا، برنامه نوشته شده بایستی همگرایی و واگرایی یک سری نامتناهی را چک کند. سپس، در صورت همگرا بودن سری، محاسبه کند که همگرایی سری به چه عددی است)

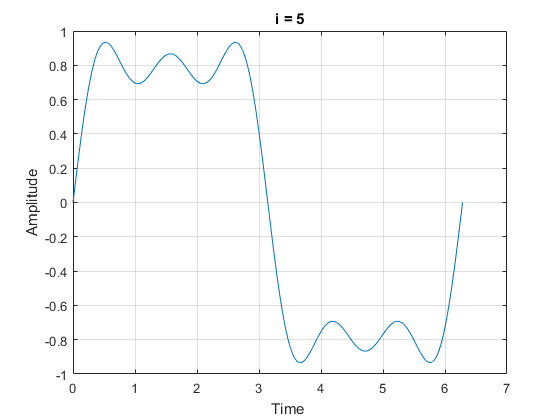
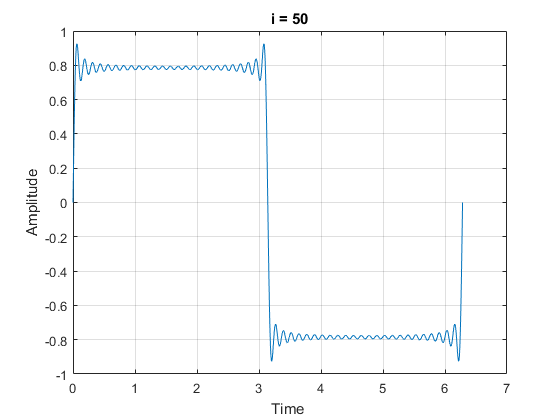
2 - تقریب تابع به کمک سری فوریه. (توضیح: برنامه نوشته شده بایستی برای هر تابع دلبخواه، سری فوریه آن تابع را محاسبه نماید. سپس، همگرایی و دقت سری را با افزایش تعداد جمالت سری مورد بررسی قرار دهد)

3 - تقریب تابع به کمک چندجمله ایهای نیوتن. (توضیح: در ابتدا، برنامه نوشته شده بایستی توابع نیوتن را محاسبه و ترسیم نماید. سپس، به کمک توابع بدست آمده، تقریبی برای هر تابع دلبخواه ورودی محاسبه نماید. سپس، همگرایی و دقت سری را با افزایش تعداد جمالت سری مورد بررسی قرار دهد)

4 - تقریب مشتق تابع به کمک روش تفاضالت محدود مرکزی. (توضیح: برنامه نوشته شده بایستی مشتق هر تابع دلبخواه را در یک دامنه خاص تابع محاسبه نماید. سپس، همگرایی و دقت روش را با افزایش تعداد نقاط مورد بررسی قرار دهد)

5 - تقریب انتگرال تابع به کمک روش ذوزنقه ای. (توضیح: در این روش، ابتدا مساحت زیر منحنی تابع به تعدادی ذوزنقه تقسیم می شود. مساحت زیر منحنی برابر خواهد بود با مجموع مساحت ذوزنقه ها. با افزایش تعداد ذوزنقه ها، دقت جواب بهبود خواهد یافت. برنامه نوشته شده بایستی انتگرال هر تابع دلبخواه را در یک بازه معین محاسبه نماید. سپس، همگرایی و دقت روش را با افزایش تعداد ذوزنقه ها مورد بررسی قرار دهد)

6 - حل معادالت دیفرانسیل معمولی مرتبه 1 به کمک روش ذوزنقه ای. (توضیح: روش ذوزنقه ای نیز یکی از ساده ترین روش ها برای حل معادلات دیفرانسیل معمولی مرتبه 1 می باشد. منتها دقت آن از روش اویلر بهتر است. در این پروژه بایستی کاربرد و دقت روش برای حل اینگونه از معادلات مورد بررسی قرار گیرد )

7 - حل معادله ریشه یابی به کمک روش نابجایی. (توضیح: روش نابجایی بسیار شبیه روش نصف کردن (برای یافتن ریشه یک تابع) می باشد. منتها، همگرایی آن سریعتر است. در این پروژه، بایستی برنامه ای به این منظور )یافتن ریشه تابع به کمک روش نابجایی) فراهم گردد (برای توضیحات بیشتر روش می توان به کتاب محاسبات عددی دکتر نکوکار مراجعه نمود)

8 - حل معادلات دیفرانسیل مرزی به کمک MATLAB( .توضیح: متلب توابع متعددی برای حل مسائل مقدار مرزی دارد. در این مسائل، مشتق ها نسبت به مختصات مکانی بیان شده اند )مثال x .)در این تحقیق، بایستی توابع مرتبط و نحوه استفاده از آنها تشریح گردند.

9 - چند جمله ایهای چبیشف. (توضیح: چندجمله ایهای چبیشف از توابع پرکاربرد در ریاضی کاربردی و محاسبات عددی هستند. این توابع از معادله دیفرانسیل هم نام (چبیشف) قابل استخراج هستند. از طرفی، روابط بازگشتی نیز برای محاسبه این توابع موجود می باشد. در این برنامه، بایستی این توابع محاسبه و ترسیم گردند.

10 - توابع بسل. (توضیح: توابع بسل از توابع پرکاربرد در ریاضی کاربردی و محاسبات عددی هستند. این توابع از معادله دیفرانسیل هم نام (بسل) قابل استخراج هستند. از طرفی، روابط ریاضی بصورت سری نیز برای محاسبه این توابع موجود می باشد. در این برنامه، بایستی این توابع محاسبه و ترسیم گردند

11 - حل معادلات دیفرانسیل معمولی زمانمند به کمک روش رانگ – کوتا. (توضیح: روش های رانگ - کوتا یکی از روش های ساده و دقیق برای حل معادالت دیفرانسیل معمولی زمانمند می باشد. در این پروژه بایستی کاربرد و دقت این روش ها برای حل اینگونه از معادالت مورد بررسی قرار گیرد)

12 - حل معادله ریشه یابی به کمک روش وتری. (توضیح: روش وتری بسیار شبیه روش نیوتن (برای یافتن ریشه یک تابع) می باشد. منتها، همگرایی آن کندتر است. در این پروژه، بایستی برنامه ای به این منظور (یافتن ریشه تابع به کمک روش وتری) فراهم گردد ( برای توضیحات بیشتر روش می توان به کتاب محاسبات عددی دکتر نکوکار مراجعه نمود)

13 - انتگرال گیری به کمک روش نقطه میانی. (توضیح: روش نقطه میانی همان روش مستطیلی برای انتگرالگیری عددی است. منتها، از نقاط میانه بازه ها برای محاسبه انتگرال کمک می گیرد. این روش بسیار مناسب است برای محاسبه انتگرال توابع منفرد ( توابعی که مثال در ابتدا یا انتهای بازه مقدار بینهایت بگیرند )  که روش مستطیلی برای محاسبه انتگرال آنها به مشکل اساسی بر می خورد. در این پروژه بایستی در قالب برنامه هایی کاربرد و دقت این روش برای تقریب انتگرال معین توابع منفرد مورد بررسی قرار گیرند

14 - انتگرال گیری به کمک روش سیمپسون. (برای توضیحات روش به کتاب محاسبات عددی دکتر نیکوکار مراجعه شود).

15 - حل سیستم معادلات جبری به کمک روش حذفی گوس و دستور کرامر. (برای توضیحات روش به کتاب محاسبات عددی دکتر نیکوکار مراجعه شود)

16 - درونیابی با استفاده از توابع Hermit

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا با متلب خونه تماس بگیرید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

پشتیبانی ( تلفن ثابت دفتر متلب خونه ) : 02191307193  

تلگرام و ایتا :  09364847193

1 - سیگنال زیر را در بازه 0 تا 2pi رسم کنید. با توجه به اینکه i عدد فرد است ، بررسی کنید هرچه i افزایش می یابد ، این سیگنال به چه سیگنالی تقریب خواهد خورد.

\[\frac{4}{\pi}\sum_{i=1}^{9}\frac{sin(i t)}{i}\]

2 - برای داده های زیر یک تابع چند جمله ای درجه 2 برازش کنید. ( ماتریس بدست آمده را با روش گوس - سایدل حل کنید )

x =  -3   0    2    4  

y =   3   1    1    3

3 -  برای داده ای زیر یک تابع نمایی به فرم y=Ae^Bx  برازش کنید.

تابع نمایی بدست آمده و داده های تابع جدولی زیر را در یک نمودار رسم کنید.

x =  0    1    2     3    4

y =  1.5  2.5  3.5  5  7.5

4 -  برنامه ای بنویسید که مجموع سری زیر را محاسبه کند. برنامه را برای m=10 و m=500 اجرا کرده و نتایج بدست آمده را با مقدار pi/4 مقایسه کنید.

( این سری ، سری لایبنیتز نامیده می شود که در مقدار pi/4  همگرا می شود )

\[\sum_{n=0}^{m}(-1)^{n}\frac {1}{2n+1} \;\;\; (n=0,1,2,...,m)\]

5 - برنامه ای بنویسید که یک ماتریس m*n تولید کند به گونه ای که تمام مولفه هی آن برابر با 1 باشند. این برنامه در واقع کاری شبیه به تابع ones (m,n) انجام می دهد.

6 - الگوریتم و فلوچارت برنامه ای را بنویسید که 10 عدد را گرفته وتعیین کند کدام زوج وکدام فرد است.

7 - برنامه ای بنویسید که 11 عدد تصادفی بین صفر و 9 تولید و زوج ، فرد یا صفر بودن هر یک را پس از تولید تعیین کند.

8 - تابعی بنویسید که یک نام ( اسامی T اشخاص ، اماکن و ... ) را دریافت کرده و در هر بار اجرا نام دریافتی را به ترتیب با حرف الفبا A,B,C, ...  کنار نام چاپ کند.

9 - داده های دما و فشار آب به صورت جدول زیر داده شده  است.

T=[0 6.8 16.8 26.8 36.8 46.8 56.8 66.8 76.8]
P=[0.006 0.009 0.019 0.035 0.062 0.105 0.171 0.271 0.416]

با استفاده از روش های درون یابی مختلف ، مقدار فشار را در دماهای 10 , 29 , 42 , 61 , 75  درجه سلسیوس و مقدار دما را به ازای فشارهای  0.01 , 0.07 , 0.1 , 0.3 بیابید.

10 - برنامه ای بنویسید که یک ماتریس m*n تولید کند به گونه ای که تمام مولفه های آن برابر 1 باشد. این برنامه در واقع کاری شبیه به تابع ones(m,n) انجام دهد.

11 - برنامه ای بنویسید که با استفاده از Matlab یک ساعت آنالوگ بسازیم.

12 - بزنامه روش حذفی گوس با محوریت نسبی قیاسی را جهت حل دستگاه معادلات خطی بنویسید(n معادله و n مجهول).

13 - بزنامه روش چولسکی را جهت حل دستگاه معادلات خطی بنویسید(n معادله و n مجهول).

14 - ماتریس زیر را بدون تایپ کردن تک تک اعداد و فقط به صورت یک خط دستوری و استفاده از  دستور linspace بسازید.

ب - از روی ماتریس تولید شده فوق و تنها با یک خط دستوری و بدون تایپ تک تک اعضا ، برداری 5 عضوی به نام B بسازید که 2 عضو اول آن ، دو عضو اول ردیف سوم ماتریس A ، و 3 عضو بعدی آن ، 3 عضو آخر ردیف اول ماتریس A باشد.

ج - فقط با استفاده از یک خط دستوری سطر دوم ماتریس A را حذف کنید.

15 - مطابق شکل مقابل ، مساحت یک مثلث بر اسا مختصات رئوس آن در سیستم مختصات کارتزین ، بر اساس رابطه زیر بدست می آید: 

با استفاده از مختصات رئوس مثلث ابتدا بردارهای OA , OB , OC را ساخته و سپس بر اساس آن ها ، مساحت مثلث را محاسبه کنید.

16 - می دانیم قانون کیرشهف برای محاسبه شدت جریان عبوری از مدار شکل مقابل به صورت زیر بیان می شود

با توجه به داده های مربوط به مدار فوق که به صورت زیر است ، جریان های مدار را به دست آورید. ( به روش حل دستگاه معادلات )

17 - رابطه زیر را به زبان متلب بنویسید ، دقت کنید که گذاشتن پرانتزهای اضافی که مورد نیاز نیستند ، نمره منفی خواهد داشت.

\[z=xln(x^{2}+y^{2}) \sqrt{\frac{y^{3}}{(y-x)^{2}}}\]

18 - دستگاه معادلات زیر را در نظر بگیرید.

مقدار z طبق رابطه زیر چقدر است؟

\[z=\frac{a^{2}+bc}{d^{3}-e}\]

19 - برنامه ای بنویسید که n عدد را بخواند و واریانس آن ها را محاسبه کند.

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.