1 - تقریبی از توابع f(x) را به ازای x چنان محاسبه کنید که خطای محاسبه کمتر از epsilon باشد.

f(x)=e^{x}cos(x) \;\;\;\;\; x=0.3235\bar{2}\;\;\;\;\; \epsilon =10^{-2}

f(x)=ln(x+1) \;\;\;\;\; x=\frac{1}{5} \;\;\;\;\; \epsilon =10^{-3}

2 - عدد 2.6  را در مبنای 2 بنویسید.

3 - تعداد ارقام با معنای اعداد 0.002014 و 12.0300 را مشخص کنید.

4 - هرگاه عدد A=5 را به صورت a=5.0074 تقریب بزنیم. عدد a چند رقم اعشار با معنا دارد؟

5 - با ذکر دلیل مشخص کنید.

الف ) تقریبی از عدد pi را چنان بنویسید تا خطای نسبی کمتر از e-4 باشد.

ب ) تقریبی از عدد pi  را چنان بنویسید تا خطای مطلق آن کمتر از e-5 باشد.

6 - حداکثر خطای منتشر شده در محاسبه ab+c² را برای مقادیر زیر با سه رقم اعشار به دست آورید.

a=\frac{2}{3},b=\pi,c=\sqrt{2}

7 - ﺗﻤﺎم ﺧﻮاص ﻣﺎﺗﺮﯾﺲﻫﺎی ﻣﺘﻌﺎﻣﺪ و ﻗﻀﺎﯾﺎی ﻣﺮﺑﻮط ﺑﻪ اﯾﻦ ﺧﻮاص را ﺑﺎ ذکر ﻣﺮﺟﻊ ﺑﻨﻮﯾﺴﯿﺪ.

8 - ﺗﻤﺎم ﻗﻀﺎﯾﺎی ﻣﻮﺟﻮد در ﻣﻮرد وﺟﻮد و ﯾکتایی ﺗﺠﺰﯾﻪ QR را ﺑﺎ ذکر ﻣﺮﺟﻊ ﺑﻨﻮﯾﺴﯿﺪ.

9 - دو اﻟگورﯾﺘﻢ ﻃﺮاحی کنید که ﺑﻪ ﺗﺮﺗﯿﺐ ﺗﺠﺰﯾﻪ QR thin و ﺗﺠﺰﯾﻪ QR ﺑﺎ ﻣﺤﻮرگیری ﺳﺘﻮنی را ﺑﺮای ﯾک ﻣﺎﺗﺮﯾﺲ دلﺧﻮاه ﺑﻪ دﺳﺖ آورﻧﺪ. ( ﺑﺪون اﺳﺘﻔﺎده از ﺗﻮاﺑﻊ آﻣﺎده، اﯾﻦ الگورﯾﺘﻢﻫﺎ را در ﻣﺤﯿﻂ پاﯾﺘﻮن  یا متلب پیاده ﺳﺎزی کنید )

10 - برنامه ای بنویسید که در ابتدا داده های یک جدول ترمودینامیکی را دریافت کند و سپس داده ی جدیدی ( هر متغیر ترمودینامیکی دلخواه ) را از کاربر دریافت کند و با توجه به آن بقیه داده های متناظر با آن را با استفاده از درونیابی و برونیابی به روش های مختلف پیدا و اعلام کند.

در نهایت با رسم نمودار (سایر انواع متغیر های ترمودینامیکی را برحسب آن نوع از متغیری رسم کنید که دریافت کردید) بگویید کدام روش خطای کمتری دارد.

توجه شود که برای هر روش باید کد آن فقط در متلب زده شود و از توابع آماده حتی االمکان استفاده نشود.

11 -  حاج ببراز خان اعتصامی 83 ساله به همراه ملوک خانم همسر 76 ساله خود قصد دارند برای شب فرزندان  خود را دعوت کنند
حاج ببراز سه پسر و سه دختر به نام‌های جهانگیر کرامت غضنفر شوکت عصمت و عفت دارد
همسر جهانگیر سعیده و پسرش علی میباشد
همسر کرامت کتایون و دخترش محدثه میباشد
همسر غضنفر ماه بانو (خواهر کتایون) و پسرش ماهان است
شوهر شوکت که برادر سعیده است
گودرز است و دختر او بهاره است

عصمت دو فرزند پسر به نام فراز و البرز
از شوهرش که به تازگی مرحوم شده به یادگاردارد
عفت جاریه عصمت است دخترش جانان وپسرش پدرام است و نام شوهرش یزدان است.
اگر حاج ببراز خان پشت میز گرد و رو به قبله بنشیند
به چند حالت این خانواده بدون اینکه محرم و نامحرم کنار یکدیگر بشینند ممکن اتفاق بیوفتد؟

12 - حل به کمک روش تکرار میرا شونده

الف ) انرژی آزاد گیبس برای اتم هیدروژن در دما T به کمک فرمول زیر قابل محاسبه است :

در صورتی که

دما مورد نیاز T برای رسیدن به این مقدار انرژی را محاسبه کنید.

13 - حل به کمک روش دلخواه به غیر از تکرار میرا شونده

معادله تعادل شیمیایی در تولید متانول از CO و  H₂ به صورت زیر است :

14 - حل انتگرال سه گانه

مطلوب است حل انتگرال سه گانه زیر به کمک روش گاوس چهار نقطه ای

15 - حل معادله دیفرانسیل مقدار اولیه

معادله زیر را به کمک روش رانج کوتای مرتبه 4 برای T=1حل کنید. گام های مختلفی برای بهبود جواب در نظر بگیرید و در پایان یک نمودار جواب نهایی بر حسب گام های h مختلف به صورت لگاریتمی رسم کنید.

در صورتی که

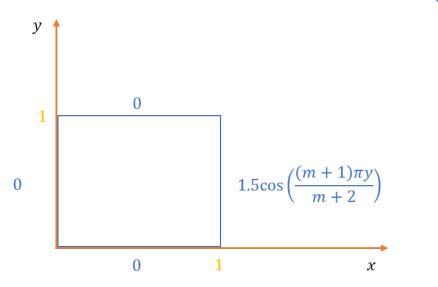
16 - حل معادله دیفرانسیل مقدار مرزی

معادله زیر را به کمک روش پرتابی حل کنیدو مقدار y(1) را بدست آورید (h=0.1) ؟

17 - بار کل Q به صورت یکنواخت بر روی حلقه توزیع شده است. یک بار نقطه ای q بر روی محور عمود بر مرکز حلثه در فاصله x قرار دارد. نیرویی که حلقه به باز نقطه ای وارد می کند از رابطه زیر بدست می آید. فاصله x زا طوری بیابید که نیرو برابر 1.5 نیوتن شود ( روش عددی دلخواه )

18 - برای حل این مساله از روش نیوتن - رافسون مرتبه دو استفاده شده است. دقت حل و حدس اولیه به عنوان ورودی از کاربر گرفته می شود. روابط به کار گرفته شده برای استفاده از این روش به صورت زیر می باشد.

19 -

20 -

جهت سفارش پروژه ، تکلیف و آموزش محاسبات عددی ، برنامه نویسی متلب MATLAB و پایتون Python لطفا با متلب خونه تماس بگیرید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

پشتیبانی ( تلفن ثابت دفتر متلب خونه ) : 02191307193  

تلگرام و ایتا :  09364847193

1 - Solve the equation with an accuracy of 10e-4 by using the secant methode

\[\begin{matrix} x^{3}-4x^{2}+2x-8=0\\ x_{0}=3\\ x_{1}=1 \end{matrix}\]
 

2 - Find a approximate root of equation in [-1,1] using Newton's method with 10e-5 accuracy.

\[e^{-x}-x^{2}-x=0\]

3 -  یک تابع بنویسید که یک عدد را دریافت کند و مشخص کند چند عدد اول کوچکتر از آن عدد وجود دارد. به عنوان مثال عدد ۱۰ را دریافت کند و عدد ۴ را نمایش دهد (۲و ۳و ۵و۷ چهار عدد اول کوچکتر از ۱۰ هستند)

4 - تابعی بنویسید که بررسی کند شماره وارد شده حتما شماره موبایل باشد. بدین صورت که تابع یک شماره تلفن را دریافت کند. بررسی کند که اولین رقم سمت چپ شماره حتما صفر باشد، در غیر این صورت پیامی چاپ کند که The number must be start zero. در مرحله دوم بررسی کند که شماره حتما یازده رقم داشته باشد، در غیر این صورت پیامی چاپ کند که   The number have must eleven digits . در مرحله سوم بررسی کند که دومین رقم سمت چپ حتما عدد 9 باشد، در غیر این صورت پیامی  The number entered is not a mobile number را چاپ کند.

5 - تابعی بنویسید که یک عدد صحیح مثبت را دریافت کند و یک ماتریس تحویل دهد. فرض کنید این عدد n باشد. با این عدد یک ماتریس مربعی n در n بسازد. درایه هایی از این ماتریس که روی قطر اصلی و فرعی ماتریس هستند، باید برابر 1 باشند و بقیه درایه ها باید برابر 0 باشند.

6 - تابعی بنویسید که از روش کرامر یک دستگاه معادلات خطی را حل کند. اگر ورودی های این تابع ماتریس A و بردار b باشد و خروجی آن بردار x باشد.

7 -  به کمک نرم افزار متلب انتگرال زیر را با روش نقطه میانی بدست آورید. ( مقدار h را 0.1 در نظر بگیرید. )

8 - به کمک نرم افزار متلب مقدار انتگرال زیر را به روش گاوس سه نقطه ای محاسبه کنید.

9 - برای محاسبه انتگرال به روش سیمپسون برنامه ای بنویسید و مقدار انتگرال زیر را بدست آورید.

| جهت سفارش پروژه و تکلیف درس محاسبات عددی و برنامه نویسی متلب MATLAB لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - یک ناحیه مربعی به اضلاع ۱ متر داریم. اضلاع فلزی هستند و ضلع سمت راست دارای ولتاژی به صورت

\[1.5cos(\frac{(m+1)\pi y}{m+2})\]

است و بقیه اضلاع به ولتاژ صفر ولت متصل شده اند. قصد داریم مقادیر ولتاژ را در نقاط مختلف به کمک MATLAB به دست بیاوریم. دقت شود m برابر با رقم راست شماره دانشجویی شما است )

2 - حل معادله حرارت

در این قسمت قصد داریم معادله حرارت را به کمک MATLAB حل کنیم. فرض کنید که میله ای به طول L داریم. ابتدای میله در مکان 0 = x و در دمای 0 درجه سانتیگراد ثابت نگه داشته شده است و انتهای میله در دمای 25 درجه. میخواهیم دمای میله را در نقاط مختلف و لحظات متفاوت به دست آوریم.

\[\frac{1}{p^{2}} \frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial t^2}\]

در معادله حرارت ضریب برابر 100 در نظر گرفته می شود  p=0.1

شرایط اولیه را به صورت مقابل در نظر بگیرید.

\[u(x,0)= \frac {2x}{1+x^{2}}\]

شرایط مرزی را به صورت مقابل در نظر بگیرید.

\[u(0,t)=0 \;\;\; \;\; u(L,t)=35\]

3 -

4 -

5 -

6 -

7 -

8 -

9 -

10 -

11 -

12 -

13 -

14 -

15 -

16 -

17 -

18 -

19 -

20 -

21 -

22 -

23 -

24 -

25 -

26 -

27 -

28 -

29 -

30 -

31 -

32 -

33 -

34 -

35 -

36 -

37 -

38 -

39 -

40 -

41 -

42 -

43 -

44 -

45 -

46 -

47 -

48 -

49 -

50 -

جهت سفارش پروژه و تکلیف درس معادلات دیفرانسیل و برنامه نویسی متلب MATLAB لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - تابع زیر را با n جمله نخست بسط تیلور این تابع حول صفر تقریب می زنیم. منحنی های تقریب زده شده را برای n=2,5,10,20 رسم کنید.

\[\begin{matrix} e^{z}\\ ln(z)\\ z^{2}+z \end{matrix}\]

2 - برنامه ای بنویسید که انتگرال معین تابع زیر را در یک بازه دلخواه با روش مستطیلی تخمین بزند. آرگومان های ورودی عبارتند از ابتدای بازه ، انتهای بازه ، و عرض مستطیل

\[\int_{a}^{b} x^{2}-3x+1\]

3 - مقدار عبارت زیر را با استفاده از فرمول تیلور تقریب بزنید.

\[ \sqrt[3]{7}\]

4 - با استفاده از فرمول مک لورن مقدار عبارت زیر را با چهار رقم اعشار درست محاسبه کنید.

\[ sin(10^\circ )\]

5 - با استفاده از سه جمله اول سری مک لورن تابع زیر را تقریب بزنید.

\[ cos(0.5 )\]

6 - نشان دهید برای هر x و y حقیقی رابطه زیر برقرار است.

\[ \left| sin(x)-sin(y)\right|\leq \left|x-y \right|\]

7 - برای سرشکنی کمترین مربعات معمولی y=3x²+2x+10  اگر

8 - تعداد دنباله های دودویی به طول n که دقیقا m بار در آن ها 01 ظاهر شده است را بیابید. n>m

9 - فرض کنید که

الف )  نمایش این عدد را در یک سیستم اعشاری معمولی 4 رقم اعشاری بنویسید.

ب ) گرد شده این عدد را در نمایش علمی 4 رقم اعشاری بنویسید.

ج ) نمایش این عدد را در یک سیستم رایانه ای 4 رقمی بنویسید.

10 - به چهار روش ( استقرا - برهان خلف - مستقیم - contraposition ) رابطه ی زیر را اثبات کنید.

11 - با استفاده از روش تکراری ژاکوبی جواب دستگاه معادلات زیر را به دست آورید. جواب اولیه را بردار صفر در نظر بگیرید و محاسبات را با 4D انجام دهید.

12 - برنامه ای بنویسید که نقاط پشتیبان را از کاربر گرفته و به عنوان خروجی درونیاب خطی را چاپ کند. تعداد نقاط پشتیبان را در ابتدا دریافت کند.

13 - برنامه ای بنویسید که نقاط پشتیبان را از کاربر گرفته و درون یابی لاگرانژ را حساب کنید و مقدار نقاط دلخواه را در تابع به دست آمده محاسبه کند.

14 -

15 -

16 -

17 -

18 -

19 -

20 -

جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

دانشجویان بر اساس جدول مشخص شده هر دانشجو اقدام به حل سوالات مشخص شده نمایند. ( پاسخ گویی به سوالات دیگر نمره نخواهد داشت )

1 - جواب عمومی معادلات دیفرانسیل را با استفاده از روش تغییر متغیر y بدست آورید.

\[\begin{matrix} y^{m}+y'=tan(x)\\ y^{n}-2y'+y=e^{2x}\\ y^{n}+4y'+4y=e^{x}\\ y^{n}+y=tan(x)\\ y^{n}-2y'+y=\frac{e^{x}}{(1-x)^{2}}\\ y^{n}-3y'+2y=ein(e^{-x}) \end{matrix}\]

2 - جواب عمومی معادلات دیفرانسیل زیر را پیدا کنید.

\[\begin{matrix} y'y^{n}=-x\\ xy^{n}=y'ln(\frac{y'}{x})\\ yy^{n}=-y'^{2}\\ (x^{2}+4)y^{n}-2xy'+2y=8\\ x^2y^n-2xy'+2y=x^{4}\\ (y-1)y^{n}=2y'^{2}\\ 2yy^{n}=1+y'^{2} \\ x^{2}y^{n}-2xy'+2y=x^{4}\\ (y-1)y^n=2y'^{2}\\ xy^{n}-(2x+1)y'+(x+1)y=(x^{2}+x-1)e^{2x}\\ x^{2}y^{n}-2xy'+2y=\frac{1}{x^{2}} \end{matrix}\]

3 - جواب معادله زیر با بیابید.

\[y'''+y'=x^{2}+6sin(2x)+xe^{3x}\]

جهت سفارش پروژه و تکلیف درس معادلات دیفرانسیل لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.