1 - حاصل هر کدام از عبارت های زیر را محاسبه کنید.
a) 3 ** 3 ** 2
b) (3 ** 3) ** 2
c) 3 ** (3 ** 2)
2 - اگر A = 6 , B = 2 and C = 3 حاصل عبارات زیر را تعیین کنید.
A/B*C
A*B/C
3*A**B
B+A/C
A/B+C
3 - آیا دستورات زیر طبق قواعد درست است؟
integer :: one = 1
one = 0
4 - حاصل عبارات زیر را تعیین کنید.
(a) 13/5*6
(b) (13/5)*6
(c) 13/(5*6)
(d) 13./(5*6)
(e) 13/5*6.
(f) INT(13./5)*6
(g) NINT(13./5)*6
(i) CEILING(13./5)*6
(j) FLOOR(13./5)*6
5 - با توجه به دستورات زیر، نوع و حاصل هر عبارت را تعیین کنید. هم چنین با اضافه کردن پرانتز به هر عبارت، ترتیب محاسبه ی عملگرها را در هر عبارت مشخص کنید.
real:: x=10.0, y=0.01, z=0.5
integer:: i=10, j=25, k=3
a1=i + j + k * i
a2=z * x / 10 + k
a3=z * k + z * j + z * i
a4=i * y - k / x + j
6 - جواب عددی دستورات زیر را تعیین کنید.
a = 9.0 / 1.5 * 0.2
b = 26 / 4 * 3
c = 26 / 4 ** 3
d = ( 10 – ( 7 – 2 ) / 3 ) / ( 7 / 4 – 5 )
e = ( 26 /4 ) ** 3
f = 2 ** ( 9 / 4 )
7- فرض کنید مقدار متغیر های زیر داده شده باشند
a=1. b=2.5 c=10. d=3. i=2 k=3
در دستور های محاسباتی زیر مقدار متغیرهای سمت چپ را بر اساس محاسبات سمت راست تعیین نمایید.
l=i/k
db=b/c
j=c/b
x = a + b / c – d
y = a + b / ( c – d ** I )
r = 3 ** k + 2 * ( I **k )
t = b ** I / c * ( c * d )
n = ( c + 2. * b ) ** i
a1 = k/i*i
da = (-c)**k – (-c)**i
8 - برنامه ای به زبان فرترن بنویسید که حقوق هفتگی یک کارگر که ساعتی کار می کند را محاسبه کند. این برنامه باید از کاربر میزان حقوق کارگر به ازای هر ساعت و ساعات کار در طول هفته را دریافت و سپس حقوق یک هفته را طبق فرمول زیر محاسبه کند.
Write a FORTRAN program that calculates an hourly employee’s weekly pay. The program should ask the user for the person’s pay rate and the number of hours worked during the week. It should then calculate the total pay from the formula:
Total Pay = Hourly Pay Rate × Hours Worked
که باید حقوق دریافتی به ازای یک هفته کار را نمایش دهد. برنامه خود را به ازای 42 ساعت کار و 7.90دلار در هر ساعت امتحان کنید.
Finally, it should display the total weekly pay. Check your program by computing the weekly pay for a person earning $7.90 per hour and working for 42 hours.
9 - انرژی پانسیل یک جسم بسته به ارتفاع آن از سطح زمین توسط معادله زیر محاسبه می شود.
UE=mgh
که در آن m جرم جسم، g شتاب گرانشی زمین و h ارتفاع آن از سطح زمین می باشد. انرژی جنبشی یک جسم در حال حرکت نیز از رابطه زیر به دست می آید:
KE=(1/2)mv2
که در آن m جرم جسم و v سرعت آن است. برنامه ای به زبان فرترن بنویسید که انرژی مکانیکی جسم را محاسبه کند (مجموع دو انرژی پتانسیل و جنبشی جسم). فرض کنید جسم در میدان گرانشی زمین قرار دارد و g = 9.81 m/s2
The potential energy of an object due to its height above the surface of the Earth is given by the equation PE = mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the height above the surface of the Earth. The kinetic energy of a moving object is given by the equation
KE=(1/2)mv2
where m is the mass of the object and v is the velocity of the object. Write a FORTRAN program for the total energy (potential plus kinetic) possessed by an object in the Earth’s gravitational field
10 - یک توپ را از حال سکون و ارتفاع h از سطح زمین رها کنیم سرعت آن هنگام برخورد با زمین توسط معادله زیر به دست می آید.
\[ v=\sqrt{2gh}\]
که در آن g شتاب گرانشی و h ارتفاع اولیه توپ از سطح زمین است (فرض کنید مقاومت هوا وجود ندارد). برنامه ای به زبان فرترن بنویسید که سرعت توپ را هنگام برخورد به زمین محاسبه کند.
If a stationary ball is released at a height h above the surface of the Earth, the velocity of the ball v when it hits the Earth is given by the equation:
\[ v=\sqrt{2gh}\]
where g is the acceleration due to gravity, and h is the height above the surface of the Earth (assuming no air friction). Write a Fortran program for the velocity of the ball when it hits the Earth.
11 - برنامه ای به زبان فرترن بنویسید که ارتفاع اولیه توپ را از کاربر دریافت کند و سپس سرعت آن را هنگام برخورد با زمین محاسبه کند (از فرمول سوال قبل استفاده کنید). برنامه را برای محاسبه سرعت توپ هنگام برخورد به زمین به ازای
الف) ارتفاع1متری
ب) ارتفاع10متری
ج) ارتفاع100متری استفاده کنید.
Write a Fortran program that calculates the velocity of the ball v when it hits the Earth from a given height h, using Equation given in previous problem. Use the program to calculate the velocity for a height of (a) 1 meter, (b) 10 meters, and (c) 100 meters.
12 - در تئوری نسبیت انیشتین، طبق معادله زیر جرم ماده با انرژی آن مرتبط است
E=mc2
که در آن E انرژی برحسب ژول، m جرم بر حسب کیلوگرم و c سرعت نور بر حسب متر بر ثانیه است،
فرض کنید که یک نیروگاه هسته ای400مگاواتی (=400میلیون ژول در ثانیه) برق یک شبکه را برای یک سال تامین می کند. برنامه ای به زبان فرترن بنویسید که جرم مصرف شده برای تولید این مقدار انرژی در طول یک سال را در نیروگاه محاسبه کند. (توجه: بازده نیروگاه را %100 فرض کنید)
In Einstein’s Theory of Relativity, the rest mass of matter is related to an equivalent energy by the equation:
E=mc2
where E is the energy in joules, m is mass in kilograms, and c is the speed of light in meters per second (c = 2.9979 × 108 m/s). Suppose that a 400 MW (= 400 million joules per second) nuclear power generating station supplies full power to the electrical grid for a year. Write a program that calculates the amount of mass consumed in the course of the year. (Note: Assume that the generating station is 100% efficient in producing electrical energy.)
13 - برنامه سوال قبل را طوری بازنویسی کنید که میزان انرژی تولید شده و بازهی زمانی (بر حسب ماه) را از کاربر دریافت کرده و سپس جرم را محاسبه کند.
Generalize the program of the previous exercise to calculate the mass consumed by a generating station with a user-specified output power for a user-specified period of months.
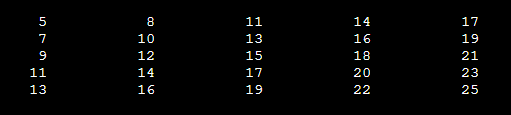
14 - برنامه ای به زبان فرترن بنویسید که مربع اعداد زوج بین 0 تا 50 را چاپ کند.
Write a Fortran program required to calculate and print out the squares of all the even integers between 0 and 50
15 - برنامه ای به زبان فرترن بنویسید که تمام مقادیر تابع بالا را برای x های بین 1- تا 3 با گام 0.1 محاسبه و چاپ کند.
Write a Fortran program to evaluate the equation y(x)=x2-3x + 2 for all values of x between −1 and 3, in steps of 0.1.
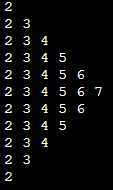
16 - حلقه های تکرار زیر را امتحان کنید و مشخص کنید هر حلقه چند بارتکرار می شود (تمام متغیرهای استفاده شده در حلقه ها را از نوع integer فرض کنید)
Examine the following DO statements and determine how many times each loop will be executed (Assume that all loop index variables are integers).
(a) DO irange = -32768, 32767
(b) DO j = 100, 1, -10
(c) DO count = 2, 3, 4
(d) DO index = -4, -7
(e) DO i = -10, 10, 10
(f) DO i = 10, -2, 0
(g) DO
17 - حلقه های تکرار زیر را بررسی و مشخص کنید که مقدار متغیر ires در پایان هر کدام ازحلقه ها چه خواهد بود. هم چنین دفعات تکرار هر حلقه را نیز مشخص کنید. تمام متغیرها را integer فرض کنید.
Examine the following iterative DO loops and determine the value of ires at the end of each of the loops, and also the number of times each loop executes. Assume that all variables are integers.
(a) ires=0
DO index=-10,10
ires=ires + 1
END DO
*************************
(b) ires=0
DO index1=10, 4, -2
DO index2=2, index1, 2
IF (index2>6) EXIT
ires=ires+index2
END DO
END DO
18 - توابع مثلثاتی معمولا به کمک سری های بی نهایت در کامپیوتر محاسبه می شوند. یک سری بی نهایت مجموعه ای از بی نهایت جمله است که با یکدیگر جمع می شوند تا مقدار یک تابع یا یک عبارت را محاسبه کنند. به عنوان مثال سری بی نهایتی که برای تقریب زدن تابع سینوس استفاده می شود عبارت است از
\[ sin(x)=\sum_{n=1}^{\infty }(-1)^{n-1} \frac{x^{2n-1}}{(2n-1)!} \]
Trigonometric functions are usually calculated on computers by using a truncated infinite series. An infinite series is an infinite set of terms that together add up to the value of a particular function or expression. For example, one infinite series used to evaluate the sine of a number is:
که در آن x بر حسب رادیان است. چون یک کامپیوتر زمان کافی برای جمع زدن بی نهایت جمله برای محاسبه سینوس هر زاویه را ندارد، تعداد محدودی ازجملات سری با هم جمع زده می شوند که به آن سری بی نهایت قطع شده می گویند. سری بی نهایت قطع شده برای سینوس به صورت زیر است
where x is in units of radians. Since a computer does not have enough time to add an infinite number of terms for every sine that is calculated, the infinite series is truncated after a finite number of terms. The number of terms that should be kept in the series is just enough to calculate the function to the precision of the floating-point numbers on the computer on which the function is being evaluated. The truncated infinite series for sin x is:
که درآن N تعداد جملاتی از سری است که جمع زده می شوند. برنامه ای به زبان فرترن بنویسید که مقدار یک زاویه را بر حسب درجه از کاربر دریافت و مقدار سینوس آن را به کمک تابع ذاتی سینوس محاسبه کند. سپس مقدار سینوس را به کمک معادله بالا به ازای N=1, 2, 3, . . . , 10محاسبه کند. مقدار درست تابع سینوس را با مقادیری که از محاسبه سینوس به کمک سری به دست می آید، مقایسه کنید. چند جمله ازسری باید با هم جمع شوند تا مقداری مساوی با مقداری که تابع ذاتی سینوس تولید می کند، ایجاد شود.
where N is the number of terms to retain in the series. Write a Fortran program that reads in a value for x in degrees, and then calculates the sine of x using the sine intrinsic function. Next, calculate the sine of x using the above equation with N=1, 2, 3, . . . , 10. Compare the true value of sin x with the values calculated using the truncated infinite series. How many terms are required to calculate sin x to the full accuracy of your computer?
19 - برنامه ای بنویسید که عدد طبیعی N را از کاربر بگیرد و ماتریس مربعی A را N در N در نظر گرفته و درایه های روی قطرهای اصلی و فرعی را یک و بقیه را صفر قرار دهد و آن را نمایش دهد.
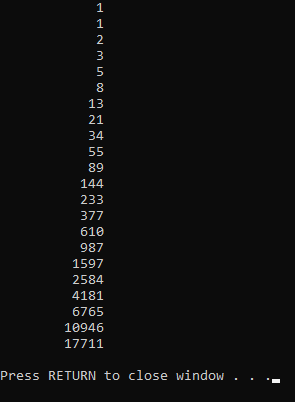
20 - با استفاده از آرایه ها، برنامه ای بنویسید که 40 جمله اول دنباله فیبوناچی (1,1,2,3,5,8,13) را محاسبه کند و نمایش دهد. یکی از خواص دنباله فیبوناچی این است که نسبت اعداد متوالی در آن (1/1,2/1,3/2,5/3,8/5) به سمت عددی موسوم به عدد طلاییSqrt(5)+1)/2) میل می کند. برنامه فوق را به گونه ای بنویسید که علاوه بر جملات دنباله، مقادیر نسبت های جملات را نیز محاسبه کند و نمایش دهد.
21 - برنامه ای بنویسید که یک ماتریس با ابعاد دلخواه را از کاربر دریافت کند و ترانهاده آن را به دست آورده و نمایش دهد.
22 - برنامه ای بنویسید که دو عدد طبیعی m و n را از کاربر بگیرد و ماتریس های A , B را به صورت m در n در نظر گرفته و حاصل جمع این دو ماتریس را محاسبه نماید.
23 - یک ماتریس مربعی متقارن است . اگر عناصر واقع در دو طرف قطر اصلی آن برابر باشند، به عبارتی دیگر خود ماتریس با ترانهاده اش یکسان باشد. برنامه ای بنویسید که عناصر یک ماتریس مربعی را دریافت کرده، معین کند ماتریس متقارن است یا نه.
24 - یک روش سریع برای محاسبه مقدار یک چندجمله ای در نقطه ای مشخص استفاده از روش هورنر یا روش ضربه ای تو در تو است. در این روش چندجمله ای را می توان به شکل زیر بازنویسی کرد. این فرم زمان کمتری از کامپیوتر برای محاسبه خواهد گرفت.
برنامه ای بنویسید که درجه چندجمله ای (n) و ضرایب چندجمله ای را بگیرد و مقدار آن را در نقاط بازه[-5,5] که به فاصله 0.5 از هم قرار دارند محاسبه و به شکل مناسبی چاپ کند.
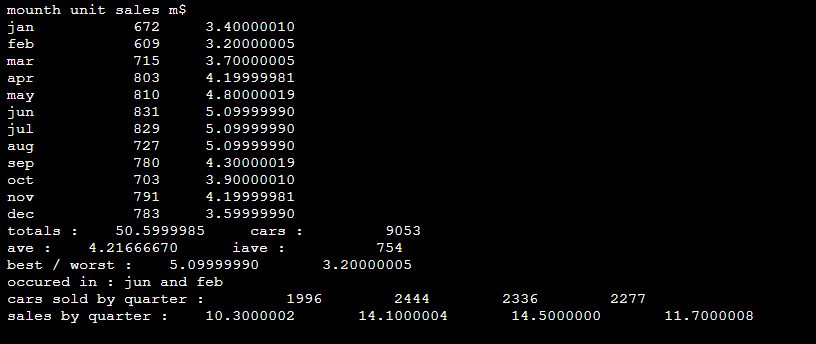
25 - برنامه ای بنویسید که برای یک مجموعه از اعداد حقیقی وارد شده توسط کاربر با استفاده از روابط زیر مقادیر میانگین، واریانس و انحراف معیار آن ها را محاسبه کند و نمایش دهد.
برنامه باید ابتدا تعداد اعداد و سپس خود اعداد را از کاربر دریافت کند. این برنامه همچنین باید موارد زیر را به عنوان خروجی نمایش دهد.
اعداد وارد شده
فاصله ی هر عدد تا مقدار میانگین
اگر یک عدد بزرگتر از مجموع میانگین و انحراف معیار باشد، برچسب خوب و اگر کمتر از مقدار میانگین منهای انحراف معیار باشد برچsب بد باید داشته باشد.
26 - برنامه ای بنویسید که اعضای دو مجموعه شامل یک سری عدد صحیح را از کاربر دریافت و سپس اجتماع و اشتراک این مجموعه ها را تعیین کند و نمایش دهد
27 - برنامه ای بنویسید که ابتدا shape یک آرایه ی با rank=2 و سپس اعضای آن را از کاربر دریافت کند و سپس مجموع عناصر هر ردیف و هر ستون را محاسبه کند و نمایش دهد.
28 - یک آرایه ی یک بعدی palindrome است اگر اعضای آن از هر دو طرف یکی باشد مثلا 3،5،7،2،4 palindrome نیست ولی 4،2،6،2،4 palindrome است. برنامه ای بنویسید که تعداد و اعضای یک آرایه ی یک بعدی را از کاربر دریافت کند و چک کند که آیا palindrome است یا خیر.
29 - برنامه ای بنویسید که تعداد و اعضای یک آرایه ی یک بعدی را از کاربر دریافت کند. سپس یک مقدار دلخواه از کاربر دریافت کند و مشخص کند که آیا این عدد دلخواه جزء المان های آرایه هست یا خیر. اگر عضوی از آن آرایه بود برنامه باید موقعیت (اندیس) المان را مشخص کند و نمایش دهد.
30 - از تابع floor می توان برای گرد کردن عددی تا تعداد مشخصی رقم اعشار استفاده کرد. دستور
y = floor( x*10 + .5 ) / 10
x را تا یک رقم بعد از اعشار و دستور
y = floor( x*100 + .5) / 100
x را تا دو رقم بعد از اعشار گرد می کند. برنامه ای بنویسید که با تعریف چهار تابع داخلی به صورت های زیر،عدد دلخواه number را گرد کند
a. round_to_integer(number)
b. round_to_tenths(number)
c. round_to_hundredths(number)
d. round_to_thousandths(number)
برنامه باید برای هر عدد دلخواهی که کاربر وارد می کند، با استفاده از تابع های بالا مقدار اولیه، عدد گردشده به نزدیک ترین عدد صحیح، عددگرد شده تا یک رقم بعد از اعشار، عدد گرد شده تا دو رقم بعد از اعشار و عدد گرد شده تاسه رقم بعد از اعشار را چاپ کند.
31 - تابعی به نام hypotenuse تعریف کنید که طول وتر یک مثلث قائم الزاویه را که دو ضلع دیگر آن داده شده اند محاسبه کند. این تابع باید دو آرگومان حقیقی و مثبت را دریافت و وتر رابه صورت یک عدد حقیقی بازگرداند. این تابع را در یک برنامه برای اضلاع دلخواه که کاربر وارد می کند، استفاده و مقدار اضلاع و وتر را چاپ کنید.
32 - تابعی داخلی بنویسید که زمان را به صورت سه آرگومان برای ساعت، دقیقه و ثانیه دریافت کند و تعداد ثانیه هایی را که از آخرین ساعت 12 گذشته بازگرداند.
33 - توابع خارجی زیر را تعریف و آن ها رادر یک برنامه پیاده سازی و استفاده کنید
الف) تابع Celsius معادل درجه سانتیگراد دمای فارنهایت را بازمی گرداند.
ب) تابع Fahrenheit معادل فارنهایت دمای سانتیگراد را بازمی گرداند.
34 - برنامه ای بنویسید که با گرفتن مقدار x از کاربر و استفاده از یک تابع خارجی برای محاسبه فاکتوریل، مقدار ex را طبق رابطه زیر محاسبه کند.
\[ e^{x}=1+\frac{1}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+...\]
35 - با استفاده از یک زیرروال به نام circle برنامه ای بنویسید که شعاع دایره ای را از کاربر بگیرد؛ قطر، محیط و مساحت آن را محاسبه و چاپ کند.
36 - برنامه ای بنویسید که مقدار یک زاویه را برحسب رادیان دریافت کند، سپس با استفاده از یک زیرروال مقدار زاویه رابه درجه، دقیقه و ثانیه تبدیل کند و نمایش دهد.
37 - برنامه ای بنویسید که یک ماتریس n*n را دریافت کند و دترمینان آن را محاسبه و چاپ نماید.
38 - برنامه ای بنویسید که با روش عددی سیمپسون Simpson انتگرال عبارت زیر را محاسبه کند.
\[ f(x)=sin(x)\]
39 - برنامه ای بنویسید که با استفاده از روش حذفی گاوس دستگاه معادلات خطی زیر را حل کند.
\[ \left\{\begin{matrix} 3x+2y+4z=4\\ 2x-3y+z=2\\x+y+2z=3\end{matrix}\right.\]
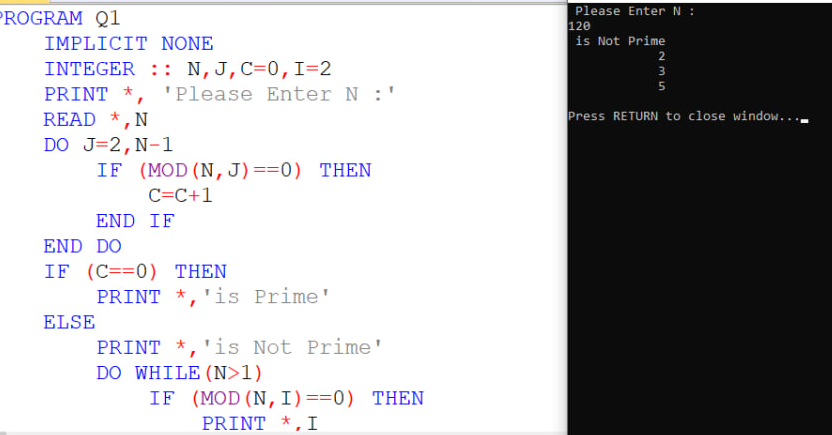
40 - برنامه ای بنویسید که عدد طبیعی N را از کاربر بگیرد و تمام اعداد اول کوچکتر از N را محاسبه و به همراه تعدادشان چاپ کند.
41 - مقدار آلودگی در شهری به این صورت اندازه گیری می شود که در ساعت 12 ظهر از سه نقطه ی شهر نمونه برداری می گردد. نقطه ی اول در یک منطقه صنعتی ، نقطهی دوم در یک منطقه مسکونی و نقطهی سوم در یک ایستگاه سیار که در شهر حرکت می کند نمونه برداری شده و داده ها به مرکز کنترل آلودگی منتقل می شود. در این مرکز ، مقدار متوسط داده های رسیده محاسبه شده و چنانچه این مقدار کمتر از 25 قسمت در میلیون 25ppm باشد ، مرکز اعلام می کند که آلودگی زیر حد خطرناک است و اگر بین 25ppm تا 50ppm باشد ، وضعیت مرکز حد وسط را اعلام می کند و در صورتی که این مقدار بیشتر از 50ppm باشد ، مرکز اعلام می کند که آلودگی به حد خطرناکی رسیده است. برنامه ای بنویسید که محاسبات مرکز کنترل آلودگی را محاسبه و نتایج را مطابق توضیحات یاد شده اعلام نماید.
42 - برنامه ای بنویسید که دو عدد طبیعی M و N را از کاربر بگیرد و ماتریس X را به صورت M در N درنظر گرفته و بردارهای A و B به ترتیب N عضوی و M عضوی را به صورت زیر ساخته و نمایش دهد.
- هر عضو بردار A برابر است با مجموع عناصر یک ستون ماتریس X
- هر عضو بردار B برابر است با مجموع عناصر یک سطر ماتریس X
43 - برنامه ای بنویسید که مختصات دو نقطه متمایز M و N از صفحه بگیرد و معادله ی خطی را که از این دو نقطه می گذرد به شکل AX+BY=C بدست آورده و نمایش دهد.
44 - سری مک لورن تابع سینوس عبارت است از
45 - برنامه ای به زبان فرترن بنویسید که 5 نقطه و مقادیر آن ها در یازه 0 تا 1 را دریافت کند و با استفاده از درونیابی لاگرانژ Lagrange مقدار درونیابی شده برای یک نقطه تست را بدست آورد.
46 - از الگوریتم حذف گوسی برای حل سیستم خطی زیر استفاده کنید و نتایج را بررسی کنید. ( دقت داشته باشید که یک عنصر روی قطر اصلی ماتریس صفر است و از الگوریتم ساده نمی توانید استفاده کنید )
47 - پروژه شامل مراحل بدست آوردن ماتریس معکوس می باشد. هر گام انجام شده را در یک سابروتین نوشته تا در گام های بعدی مورد استفاده قرار گیرد. کدنویسی فقط در زبان برنامه نویسی فرترن انجام گیرد.
الف ) برنامه ای بنویسید که یک ماتریس دلخواه از مرتبه 5 را دریافت و دترمینان آن را بدست آورد.
ب ) حال برنامه ای بنویسید که ماتریس کهاد مرتبط با ماتریس ورودی را بدست آورد. (جهت بدست آوردن درایه ماتریس کهاد، روی سطر و ستون مرتبط با هر درایه، خطی بکشید و دترمینان ماتریس حاصل از حذف آن سطر و ستون را بیابید و دترمینان محاسبه شده را در درایه مرتبط ماتریس قرار دهید.)
ج ) حال ماتریس همسازه را بدست آورید. برای بدست آوردن ماتریس همسازه کافی است تایکی در میان عالمت درایه های ماتریس کهاد در 1-ضرب شوند. بعبارتی هر درایه از ماتریس کهاد، ضرب در منفی یک به توان مجموع سطر و ستون آن درایه گردد.
د ) حال ماتریس الحاقی را بدست آورید. ماتریس الحاقی در حقیقت همان ترانهاده ماتریس همسازه است
ه ) اکنون ماتریس معکوس را با ضرب 1 تقسیم بر دترمینان ماتریس و ماتریس الحاقی بدست می آید.
48 - می خواهیم توزیع دما در حالت پایا روی سطح دو بعدی زیر در فواصل 1cm در راستاهای x و y را بدست آوریم.
معادله دیفرانسیلی توزیع دما ( با تولید حرارت ، غیر پایا ، سه بعدی )
معادله دیفرانسیلی توزیع دما ( بدون تولید حرارت ، پایا ، دو بعدی )
معادله گسسته سازی شده توزیع دما در حالت پایا ( بدون تولید حرارت ) و دو بعدی
49 - برنامه ای بنویسید که یک عدد صحیح را به عنوان ورودی بگیرد و بررسی کند آیا این عدد اول است یا خیر. اگر عدد اول نیست، تمامی فاکتورهای آن را به ترتیب صعودی نمایش دهد.
50 - برنامه ای را بنویسید که مقدار x را خوانده و y را بر اساس موارد زیر محاسبه کرده و نمایش دهد.
\[y=\left\{\begin{matrix}5+e^{\sqrt{x}};x>0\\arcsin^{2}(x+1);x=0\\\sqrt[3]{x+5};x<0\end{matrix}\right.\]
51 - برنامه ای به زبان فرترن FORTRAN بنویسید که طول طولانی ترین دنباله اعداد صعودی متوالی در یک آرایه را پیدا کند.
52 - برنامه ای بنویسید که تمام عناصر یک ماتریس را به اندازه یک خانه در جهت عقربه های ساعت بچرخاند. به طوری که عناصر در هر سطر و ستون به سمت راست منتقل شوند.

53 - اگر یک توپرا از حال سکون و ارتفاع h از سطح زمین رها کنیم، سرعت آن هنگام برخورد با زمین توسط معادله زیر به دست می آید.
\[v=\sqrt{2gh}\]
که در آن g شتاب گرانش و h ارتفاع اولیه توپاز سطح زمین است. برنامه ای به زبان فرترن بنویسید که ارتفاع اولیه توپ را از کاربر دریافت کند و سپس سرعت آن را هنگام برخورد با زمین محاسبه کند. برنامه را برای محاسبه سرعت توپ هنگام برخورد به زمین به ازای الف ) ارتفاع 1 متری ب ) ارتفاع 10 متری ج ) ارتفاع 100 متری استفاده کنید. g=9.81m/s2
54 - ابتدا یک برنامه به زبان فرترن بنویسید که x و y از کاربر دریافت کند و به کمک یک ساختار 4 حاله if مقدار f(x,y) را محاسبه کند و سپس برنامه خود را بازنویسی کنید و به کمک if های تو در تو مقدار f(x,y) را محاسبه کنید. برنامه باید به گونه ای نوشته شود که بخش خارجی شروط x را مورد ارزیابی قرار دهد و بخش داخلی شروط y را بررسی کند. مطمئن شوید که به هرکدام از بخش های برنامه خود نام اختصاص دهید.
\[\left\{\begin{matrix}f(x,y)=x+y& x>0,y>0 \\f(x,y)=x+y^{2}& x>0,y<0 \\f(x,y)=x^{2}+y &x<0,y>0 \\ f(x,y)=x^{2}+y^{2}& x<0,y<0 \\\end{matrix}\right.\]
55 - برنامه ای به زبان فرترن بنویسید که تمام مقادیر تابع y(x)=x2 -3x+2 را برای x های بین 1- تا 3 با گام 0.1محاسبه و چاپ کند.
56 - حلقه های تکرار زیر را بررسی و مشخص کنید که مقدار متغیر res در پایان هر کدام از حلقه ها چه خواهد بود. همچنین دفعات تکرار هر حلقه را نیز مشخص کنید. تمام متغیرها را integer فرض کنید.
ires=0
DO index=-10,10
ires=ires+1
END DO
ires=0
DO index1=10,4,-2
DO index2=2,index1,2
IF (index2>6) EXIT
ires=ires+index2
END DO
END DO
57 - برنامه ای بنویسید که با گرفتن مقدار x از کاربر و استفاده از یک تابع خارجی برای محاسبه فاکتوریل، مقدار ex را طبق رابطه زیر محاسبه کند. سپس مجدد برنامه را با استفاده از یک زیرروال ( سابروتین - زیربرنامه ) بنویسید.
\[e^{x}=1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+...\]
58 - یک ماتریس مربعی متقارن است اگر عناصر واقع در دو طرف قطر اصلی آن برابر باشند، به عبارتی دیگر خود ماتریس با ترانهاده اش یکسان باشد. برنامه ای بنویسید که عناصر یک ماتریس مربعی را دریافت کند و بررسی کند که آیا متقارن است یا خیر.
59 -
جهت سفارش پروژه ، تکلیف و آموزش فرترن Fortran لطفا با متلب خونه تماس بگیرید، تا پس از بررسی هزینه خدمت شما اعلام گردد.
پشتیبانی ( تلفن ثابت دفتر متلب خونه ) : 02191307193
تلگرام و ایتا : 09364847193