1 - روش گاوس سایدل در جبر خطی عددی روش تکراری است که برای حل دستگاه معادلات خطی استفاده میشود.
اگرچه از این روش میتوان در هر ماتریسی که دارای درایه قطری صفر نباشد استفاده کرد، اما فقط در صورتی همگرایی تضمین میشود که ماتریس مثبت معین یا قطریغالب باشد.
( کد نوشته شده ابتدا با دریافت دو ماتریس A و B و تعداد تکرار n ، مقدار x را در مرتبه n تکرار محاسبه می کند.
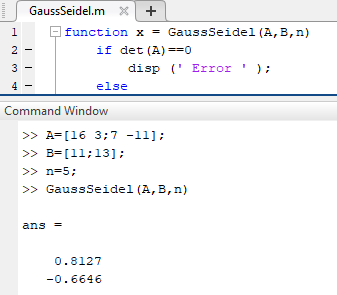
2 - به روش های ژاکوبی و گاوس سیدل جواب دستگاه زیر را بدست آورید.
\[\left\{\begin{matrix} x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=1\\ x_{1}+2x_{2}+3x_{3}+4x_{4}+5x_{5}=0\\ x_{1}+3x_{2}+6x_{3}+10x_{4}+15x_{5}=0\\ x_{1}+4x_{2}+10x_{3}+20x_{4}+35x_{5}=0\\ x_{1}+5x_{2}+15x_{3}+35x_{4}+70x_{5}=0 \end{matrix}\right.\]
نکته مهم در این سوال چک کردن شرط همگرایی روش گاوس سیدل است.
روش گوس سایدل همگرا است، اگر:
الف - ماتریس ضرایب یک ماتریس مثبت معین متقارن باشد،
ب - ماتریس ضرایب اکیداً غالب قطری باشد.
ماتریس ضرایب این دستگاه هیچ کدام از دو شرط بالا را ندارد. پس روش گاوس سیدل همگرا نشده و جواب نمی دهد و فقط می توان از روش ژاکوبی استفاده کرد.

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.