1 - بازی مین روب Minesweeper
بازیهای مینروب minesweeper یکی از اولین بازیهایی بود که روی کامپیوترها تجربه کردیم. اولین بازی با این شکل و شمایل در سال ۱۹۶۰ منتشر شد و هنوز هم طرفداران خودش را دارد. بازیهای مینروب بر اساس تصمیمات منطقی بازیکن جلو میروند که باید تمام مینها را کشف کند و حواسش باشد که روی آنها کلیک نکند. برای این کار باید از اعدادی که روی هرخانه نوشته شده استفاده کنید که نشان میدهند چند مین در اطراف آن خانه وجود دارد.
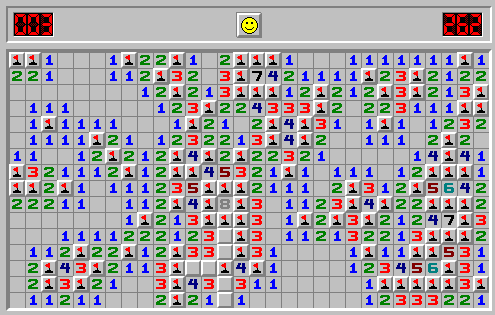
با استفاده از متلب قصد داریم بازی MineSweeper را به دو صورت آنالوگ و گرافیکی پیاده سازی کنیم.
در پیاده سازی آنالوگ ابتدا کاربر درجه سختی و سایز بازی را وارد می کند.
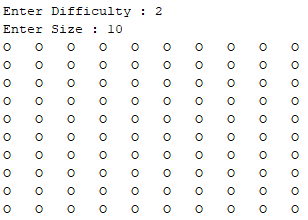
در مرحله بعد دو بازیکن به ترتیب مختصات نقاط دلخواه را وارد می کنند.
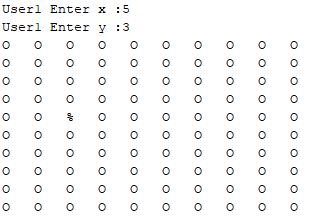
اگر مین نباشد علامت درصد را نشان می دهد و نوبت به بازیکن بعدی می رسد.
این روند تا جایی ادامه میابد که یک یازیکن مین را انتخاب کند و بازی با معرفی برنده و بازنده پایان یابد. در پایان نقشه ی کل مین ها نمایش داده می شود.
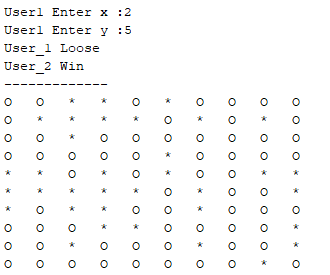
در حالت گرافیکی ابتدا درجه سختی از کاربر دریافت می شود و بر اساس درجه سختی سایز و تعداد مین ها مشخص می شود.
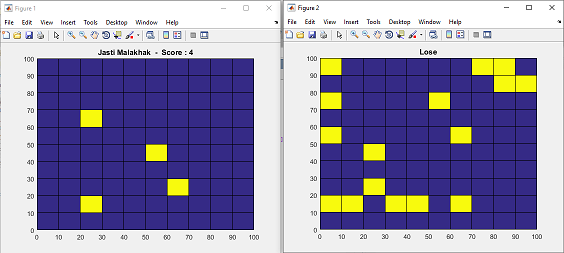
در هر مرحله کاربر یک خانه را انتخاب می کند. در صورتی که مین نباشد عبارت Jasti Malakhak نوشته شده و یک واحد به Score افزوده می شود. در صورتی هم که مین باشد عبارت Lose نوشته شده و نقشه کل مین ها نمایش داده می شود.
2 - نمودار sinh , cosh و tanh را در یک محور در محدوده ی 1- تا 1 رسم کنید. سپس هر نمودار را با رنگی متفاوت مشخص کرده و برای هر نمودار برچسبی با متن و فلش ( پیکان ) در محل مناسب قرار دهید.

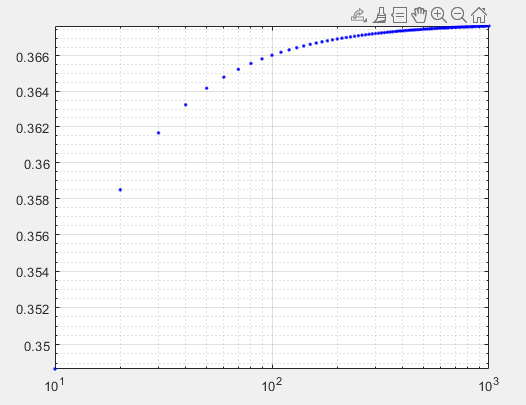
3 - اتحاد زیر را به خاطر آورید. یک نمودار لگاریتمی log-log بر حسب n=10,20,30,...,1000 رسم کنید. از این نمودار چه پیش بینی در مورد رفتار مجانبی دارید.
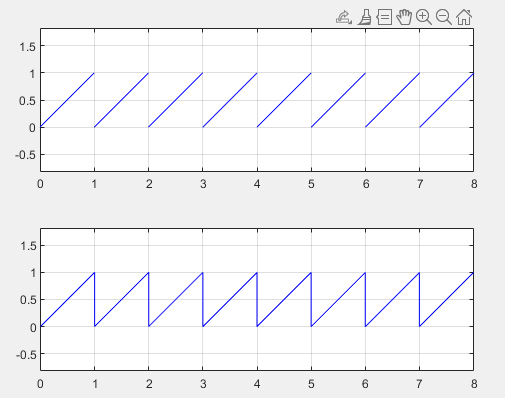
4 - دو روش نمایش تابع موج دندان اره ای در زیر آورده شده است. با دقت توضیح دهید چرا این دو متفاوت اند.
>> x = [0:7;1:8]; y = [zeros(1,8);ones(1,8)];
>> subplot(211), plot(x,y,'b'), axis equal
>> subplot(212), plot(x(:),y(:),'b'), axis equal
5 - بازی هرج و مرج را انجام دهید. فرض کنید P1, P2, P3 سه راس یک مثلث باشندو با یک نقطه دلخواه درون مثلث شروع کنید. به صورت اتفاقی یکی ار زئوس مثلث را انتخاب کرده و به اندازه نصف فاصله تا آن راس حرکت کنید. حال از نقطه جدید دوباره همین عمل را تکرار کنید و سعی کنید تا جایی که می توانید ( از نظر ریاضی تا بی نهایت و از نظر فیزیکی تا اعداد بسیار بزرگ ) ادامه دهید. اگر موقعیت هر نقطه از شکل را علامت گذاری کنید، الگوی تکرار شونده Fractal را خواهید یافت.

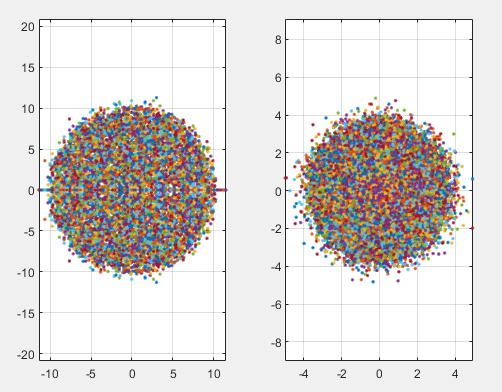
6 - تفاوت کیفی دو نمودار حاصل از نمایش های زیر را توصیف کنید.
الف ) 100 عدد ماتریس اتفاثی با فرمان randn(100) ایجاد کنید و مقادیر ویژه آن ها را در یک نمودار بصورت نقاطی نمایش دهید. ( باید 10000 نقطه داشته باشید ). از فرمان axis equal برای تغییر منظر دید به حالت یک به یک استفاده کنید.
ب ) حالت الف را با ایجاد یک نمودار جدید تکرار کنید اما این بار 100 ماتریس از اعداد اتفاقی مختلط با دستور complex(randn(100),rand(100) ایجاد کنید.
7 - نمودار رویه های زیر را در محدوده ی داده شده رسم کنید.
8 - نمودار کانتوری توابع داده شده در مساله قبل را رسم کنید.
9 - یک نمودار کانتوری برای تابع زیر رسم کنید.
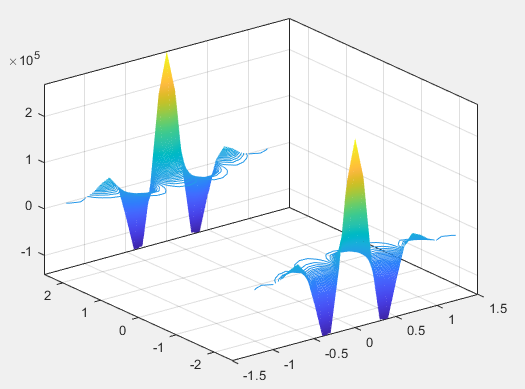
10 - نمودار رویه ای که با تابع زیر در محدوده مشخص شده را رسم کنید.
جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.