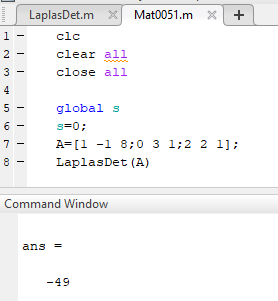
1 – یک تابع (تابع تعریفی از سوی کاربر) بنویسید که دترمینان یک ماتریس 3×3 را با استفاده از رابطه زیر محاسبه کند:
از det3by3(A)= d3 برای نام و پارامترهای تابع استفاده کنید. پارامتر ورودی A ماتریس مورد نظر بوده و پارامتر خروجی d3 مقدار دترمینان می باشد. برنامه ی مربوط به det3by3 را به گونها ی بنویسید که از یک زیر تابع برای محاسبه دترمینان ماتریس 2×2 استفاده نماید.
2 - تابع \[y=3x^{3}-26x+10\] و مشتقات اول و دوم آن را به ازای \[-2\leq x\leq 4\]
الف - درون یک شکل رسم نماید.
ب - درون چند شکل در یک صفحه رسم نماید.
ج - در پنجره های شکل متفاوت رسم نماید.
دقت شود که در هر سه حالت محورها نامگذاری شوند، عنوان شکل تعیین شود، در قسمت الف و ب بخش مربوط به معرفی منحنی نیز اضافه شود.
3 – یک مقاومت با مقدار \[R=4\Omega\] و یک سلف با مقدار \[L=1.3 H\] همان گونه که در شکل الف مشاهده می شود، در یک مدار به یک منبع ولتاژ متصل شده است ( مدار RL )
زمانی که منبع ولتاژ، یک ولتاژ پالسی مستطیلی با اندازه \[V=12v\] و بازه ی \[-0.5 s\]همانگونه که در شکل ب مشاهده می شود – به مدار اعمال نماید، جریان \[i(t)\] در مدار به صورت تابعی از زمان با روابط زیر نشان داده می شود:
\[\begin{matrix} i(t)=\frac{V}{R}(1-e^{(-Rt)/L}) & 0\leq t\leq 0.5 \\ i(t)=e^{(-Rt)/L}\frac{V}{R}(e^{(0.5R)/L}-1) &0.5\leq t \end{matrix}\]
منحنی جریان را به صورت تابعی از زمان برای بازه ی \[0\leq t\leq 2\] رسم نمایید.
| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.