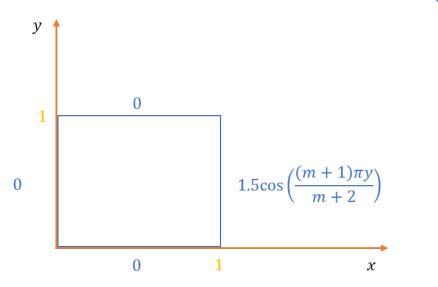
1 - یک ناحیه مربعی به اضلاع ۱ متر داریم. اضلاع فلزی هستند و ضلع سمت راست دارای ولتاژی به صورت
\[1.5cos(\frac{(m+1)\pi y}{m+2})\]
است و بقیه اضلاع به ولتاژ صفر ولت متصل شده اند. قصد داریم مقادیر ولتاژ را در نقاط مختلف به کمک MATLAB به دست بیاوریم. دقت شود m برابر با رقم راست شماره دانشجویی شما است )
2 - حل معادله حرارت
در این قسمت قصد داریم معادله حرارت را به کمک MATLAB حل کنیم. فرض کنید که میله ای به طول L داریم. ابتدای میله در مکان 0 = x و در دمای 0 درجه سانتیگراد ثابت نگه داشته شده است و انتهای میله در دمای 25 درجه. میخواهیم دمای میله را در نقاط مختلف و لحظات متفاوت به دست آوریم.

\[\frac{1}{p^{2}} \frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial t^2}\]
در معادله حرارت ضریب برابر 100 در نظر گرفته می شود p=0.1
شرایط اولیه را به صورت مقابل در نظر بگیرید.
\[u(x,0)= \frac {2x}{1+x^{2}}\]
شرایط مرزی را به صورت مقابل در نظر بگیرید.
\[u(0,t)=0 \;\;\; \;\; u(L,t)=35\]
3 -
4 -
5 -
6 -
7 -
8 -
9 -
10 -
11 -
12 -
13 -
14 -
15 -
16 -
17 -
18 -
19 -
20 -
21 -
22 -
23 -
24 -
25 -
26 -
27 -
28 -
29 -
30 -
31 -
32 -
33 -
34 -
35 -
36 -
37 -
38 -
39 -
40 -
41 -
42 -
43 -
44 -
45 -
46 -
47 -
48 -
49 -
50 -
جهت سفارش پروژه و تکلیف درس معادلات دیفرانسیل و برنامه نویسی متلب MATLAB لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.