1 - سری فوریه تابع متناوب زیر را با دوره تناوب T=2pi بنویسید.
\[f(x)=\left\{\begin{matrix} 1+\frac{2}{\pi}x & -\pi\leq x< 0\\ 1-\frac{2}{\pi}x & 0\leq x< \pi \end{matrix}\right.\]
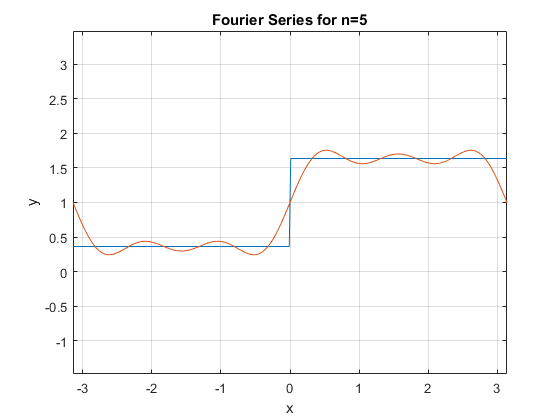
2 - سری فوریه تابع متناوب زیر را با دوره تناوب T=2piبدست آورید. و با استفاده از قضیه مشتق گیری از سری های فوریه ، سری فوریه f(x)=x را بدست آورید.
\[f(x)=x^{2}\;\;\;\; -\pi<x<\pi\]
3 - بسط سینوسی تابع زیر را در بازه خواسته شده بدست آورید.
\[f(x)=\pi+x \;\;\;\; 0<x<\pi\]
4 - سری فوریه مختلط تابع متناوب زیر را در بازه خواسته شده بدست آورید.
\[f(x)=x \;\;\;\; 0<x<2\pi\]
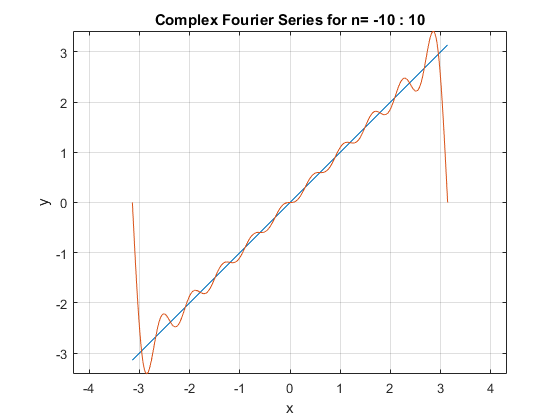
5 - انتگرال فوریه تابع مقابل را به دست آورید.
\[f(x))=\left\{\begin{matrix} x^{2} &\left | x \right | <1\\ 0 & \left | x \right | >1 \end{matrix}\right.\]
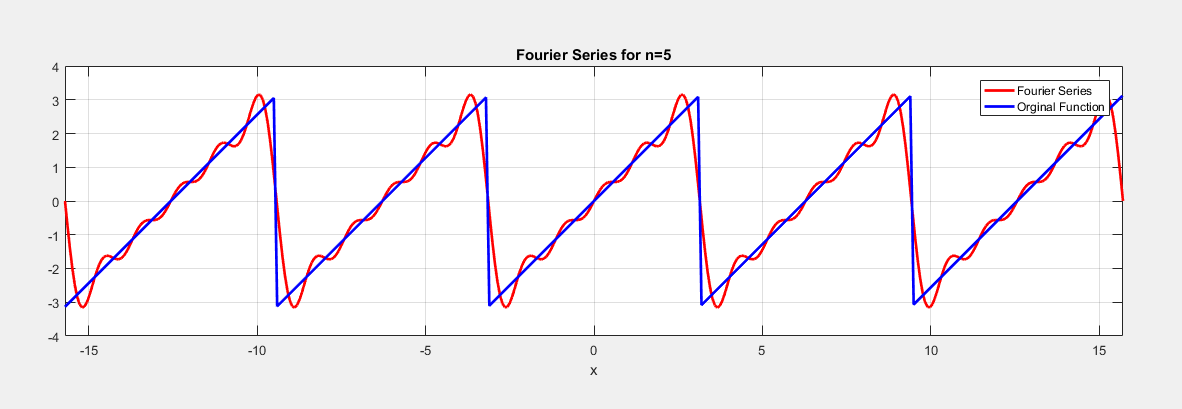
6 - سری فوریه تابع پله زیر را به ازای 4 ، 10 و 50 جمله محاسبه و رسم نمایید.
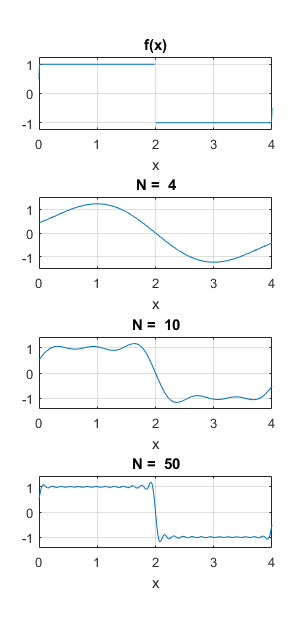
7 - برنامه ای بنویسید که یک تابع و یک نقطه را دریافت کند و بسط تیلور تابع را در آن نقطه محاسبه کند.
8 - بسط فوریه سینوسی و کسینوسی تابع y=1-x را رسم کنید و تفاوت را بررسی کنید.
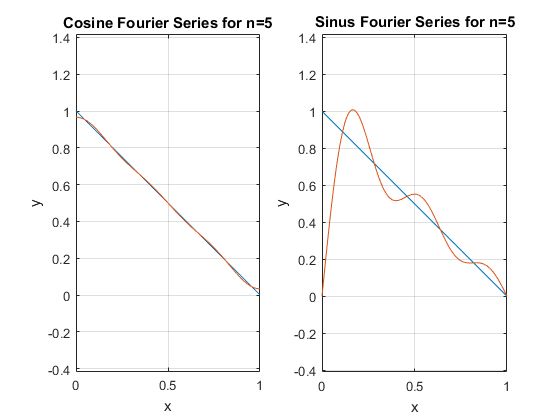
9 - بسری فوریه تابع f(x)=x را به صورت متناوب رسم کنید.
10 - به نقطه وسط یک میله فلزی قابل ارتعاش به طول 5 که بدون انحنا و به صورت خط مستقیم قرار دارد با یک چکش ضربه ای وارد می شود به طوری که در این میله سرعت اولیه معادل g(x) ایجاد می شود.
در این میله نیروی کشسانی در راستای افق برابر 3.5 و جرم 3.5 و جرم واحد طول 12 است. بعد از دو ثانیه این ضربه تکرار می شود و بعد از 5 ثانیه مجدد تکرار می گردد.
معادله ارتعاش این میله در 5 ثانیه اول و بعد از آن را بدست آورده و ارتعاش میله را توسط کامپیوتر به صورت تصویر متحرک نشان دهید.
( میله به صورت خطی و بدون بعد در نظر گرفته شده و از اصظکاک و سایر نیروهای مقاوم صرف نظر می شود. )
جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.
