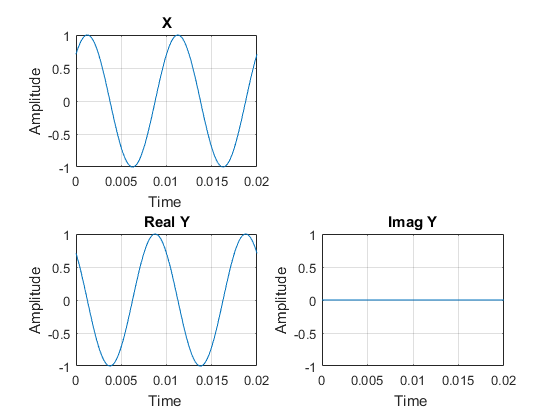
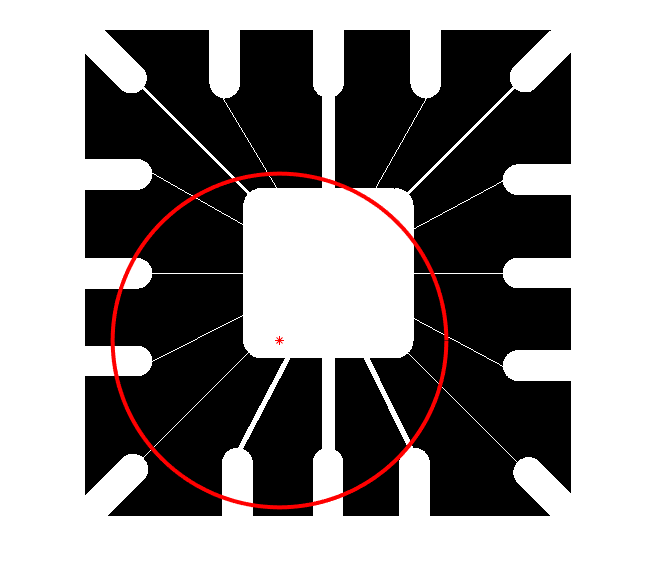
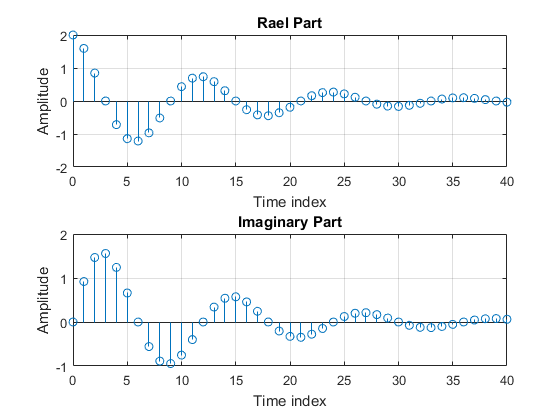
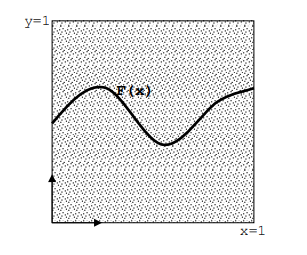
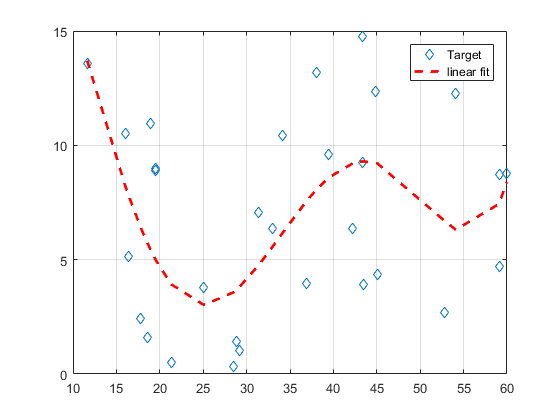
1 - با نوشتن کد در نرم افزار متلب ، ابتدا رابطه دو ضابطه ای سیگنال x(t) که در شکل زیر نشان داده شده است را بنویسید. سپس در شکل های جداگانه نمودارهای زیر را رسم کنید.
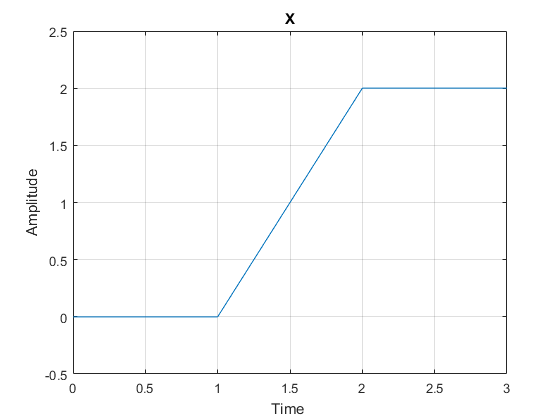
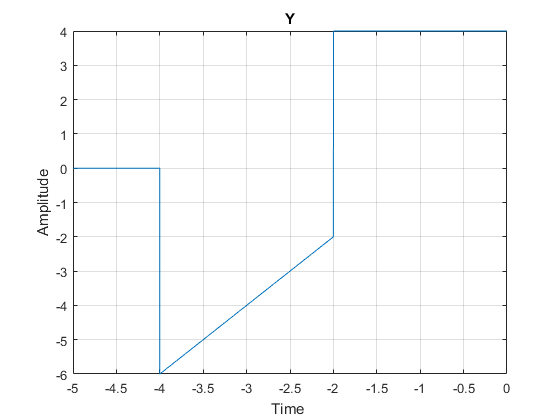
در مرحله بعد y را رسم می کنیم.
\[y(t)=2x(0.5t+3)\]
2 - تابعی با عنوان زیر بنویسید، به نحوی که x یک بردار و out برابر با 10 المان زوج ابتدایی x است. اگر تعداد المان های زوج بردار x کمتر از 10 باشند، مقادیر 0 جایگزین شوند تا اندازه خروجی برابر 10 شود.
[out]=myMakeSize10(x)
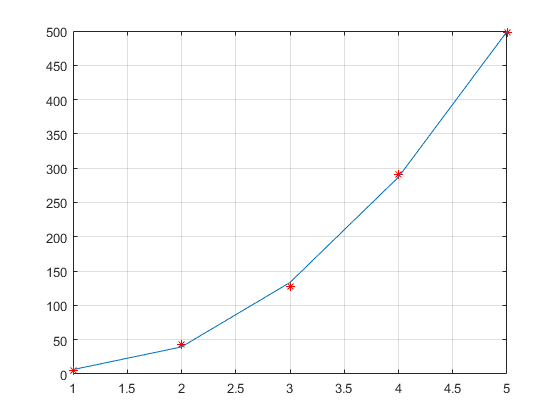
3 - تابعی بنویسید که یک چند جمله ای ( به صورت یک بردار سطری ) و یک بردار دو عنصری ( حاوی دامنه ترسیم ) را از کاربر بگیرد و نمودار چند جمله ای را در دامنه مشخص شده ترسیم کند.
تابع فوق را طوری تغییر دهید که اگر با دو آرگومان خروجی به کار برده شود، به جای ترسیم مقادیر x و y محاسبه شده را بازگرداند.
4 - برنامه ای بنویسید که یک ماتریس دو بعدی دلخواه را از ورودی دریافت کرده و بزرگترین ماتریس مربعی موجود در ماتریس ورودی که مجموع عناصر موجود روی قطر اصلی آن مضرب 3 باشد را به عنوان خروجی برگرداند.
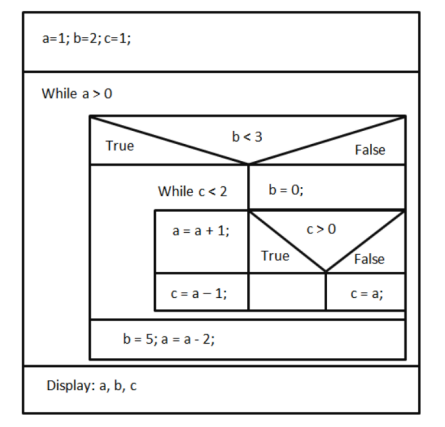
5 - الگوریتم و فلوچارتی بنویسید که یک ماتریس دو بعدی را دریافت کند و سایز آن را تعیین کند.
6 - فلوچارتی رسم کنید که یک عدد صحیح از ورودی دریافت و مشخص کند برای خرد کردن چنین مقدار پولی با سکه های یک تومانی ، 2 تومانی و 10 تومانی به حداقل چه تعداد سکه نیازمندیم.
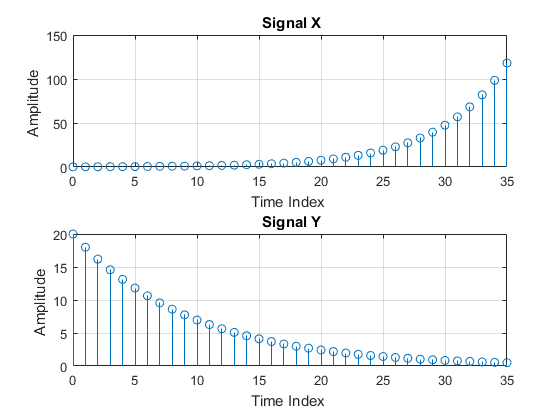
7 - برنامه ای بنویسید که با دریافت سه تابع تبدیل از کاربر ، خروجی آن را نسبت به سه ورودی تصادفی 20*1 محاسبه کند. سپس هر سه خروجی را بر روی یک نمودار رسم کند.
راهنمایی : برای بدست آوردن خروجی یک سیستم نسبت به یک ورودی از دستور زیر استفاده کنید.
با فرض t=1:20
خروجی = lsim (نام بردار ورودی , نام تابع تبدیل , t);
8 - برنامه ای بنویسید که در آن سیستم 10 عدد تصادفی بین 1 تا 100 را تولید نماید و کاربر بتواند 5 بار اعداد را حدس بزند. اگر کاربر بتواند در 5 بار تلاش 2 عدد تصادفی تولید شده را تشخیص دهد برنده و در غیر این صورت بازنده خواهد بود.
9 - برنامه ای بنویسید که یک بردار از اعداد را گرفته و تمام زیر مجموعه های دو عضوی آن را در ماتریس دیگری چاپ کند.
\[A=[2 \;\; 4 \;\;7\;\; 6]\]
\[B=\begin{bmatrix} 2&4 \\ 2 & 7\\ 2& 6\\ 4& 7\\ 4& 6\\ 7& 6 \end{bmatrix}\]
10 - برنامه ای بنویسید که عدد صحیح و مثبت ( مثلا n ) را از کاربر گرفته و اعدا صحیح و مثبتی که حاضلضرب آن ها کوچکتر از این عدد است را بیابد و خروجی برنامه اعداد فوق و تعداد آن ها می باشد. مثلا برای ورودی عدد 25 خروجی برنامه باید اعداد 1 و 2 و 3 و 4 باشد.
11 - برنامه ای بنویسید که n عدد صحیح مثبت از ورودی بخواند سپس عددی که مجموع ارقام اول آن از همه بیشتر است را در خروجی چاپ کند.
12 - برنامه ای بنویسد که عددی در مبنای a از ورودی بخواند سپس معادل مبنا b آن را چاپ کند.
13 - برنامه ای بنویسید که n عدد از ورودی بخواند سپس میانگین اعداد مثبت و منفی را جداگانه در خروجی چاپ کند.
14 - برنامه ای بنویسید که دو عدد صحیح و یک عملگر ریاضی ( + و - و * و / ) را به عنوان ورودی از صفحه کلید بگیرد و بعد از انجام هر عملیات ریاضی و چاپ نتیجه از کاربر سوال نماید. می خواهید ادامه دهید یا خیر. در صورت مثبت بودن جواب فرآیند تکرار شود و در صورت منفی بودن پاسخ ، برنامه به اتمام برسد.
15 - برنامه ای بنویسید که یک عدد از کاربر بگیرد و آن را به عوامل اول تجزیه کند.
16 - فرض کنید بخواهیم انتگرال زیر را با خطایی حداکثر 0.001 محاسبه کنیم.
\[f(x)=\int_{0}^{1}sin(\frac {\pi x^{2}}{2})dx\]
الف ) با روش ذوزنقه ای بازه [0,1] را حداقل به چند زیر بازه باید تقسیم نمود؟
ب ) با روش سیمپسون بازه [0,1] را حداقل به چند زیر بازه باید تقسیم نمود؟
17 - برازش خطی Linear Fitting : فرض کنید یک سری x و y به ما داده اند و از ما می خواهند که بهترین خط عبوری از آنها را بدست آوریم . در کد نوشته شده حتما x و y را وارد کنید. نه اینکه آن را از کاربر بگیرد ، همچنین لطفا طوری کد را طراحی کنید که با کم و زیاد کردن ماتریس های x و y کد قابلیت اجرا داشته باشد.
18 - برنامه ای بنویسید که تعداد درس اخذ شده توسط یک دانشجو در یک ترم را دریافت نموده ، با ورود نمرات و نعداد واحد هر درس، معدل آن دانشجو را حساب کنید.
الف ) تعداد درس اخذ شده در یک ترم
ب ) تعداد دروس بالای 18
ج ) تعداد دروس پاس شده زیر 15
د ) تعداد دروس پاس نشده
19 - برنامه ای بنویسید که یک عدد مثبت را دریافت کند و همه مقسوم علیه های آن را نمایش دهد.
20 - برنامه ای بنویسید که عدد صحیح n را دریافت کرده و حاصل جمع n جمله ی اول سری زیر را نمایش دهد.
\[S=\frac {1}{1!}+\frac {2}{2!}+\frac {3}{3!}+...+\frac {N}{N!}\]
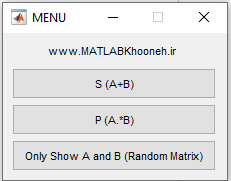
21 - برنامه ای بنویسید که دو بردار تصادفی به طول 10 از اعداد صحیح کوچکتر از 30 ایجاد کند. سپس یک منو در نرم افزار متلب ایجاد کنید. در صورت کلیک بر روی دکمه اول حاصل جمع درایه به درایه را برگرداند. در صورت کلیک بر روی دکمه دوم حاصل تفریق درایه به درایه را چاپ نماید و در صورت کلیک بر روی دکمه سوم هر دو بردار را برگرداند.
22 - برنامه ای بنویسید که یک دایره به شعاع 10 واحد را در نظر بگیرد. سپس دو دایره به شعاع 5 واحد یکی محاط و یکی محیط ( داخل و بیرون دایره اصلی ) در نظر گرفته شود. در مرحله بعد دو دایره کوچک در خلاف جهت یکدیگر بر روی دایره بزرگ حرکت کنند.
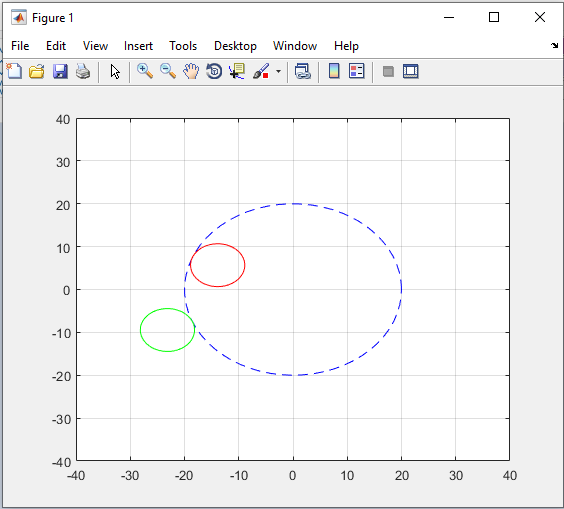
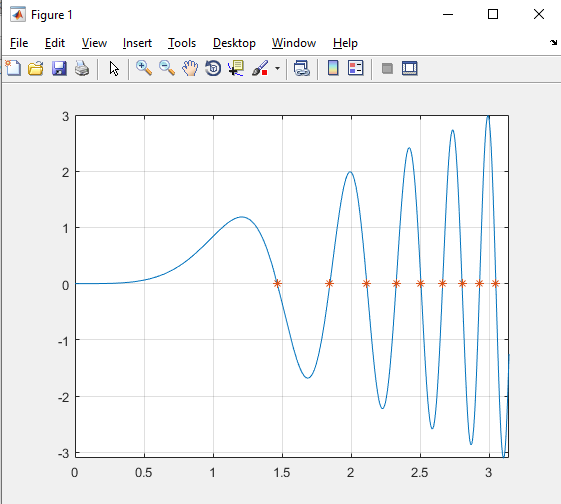
23 - برنامه ای بنویسید که با استفاده از روش تصادفی مونت کارلو ریشه های معادله x sin(x3) را بدست آورد. هدف پیاده سازی روش مونت کارلو برای پیدا کردن ریشه های معادلات است.
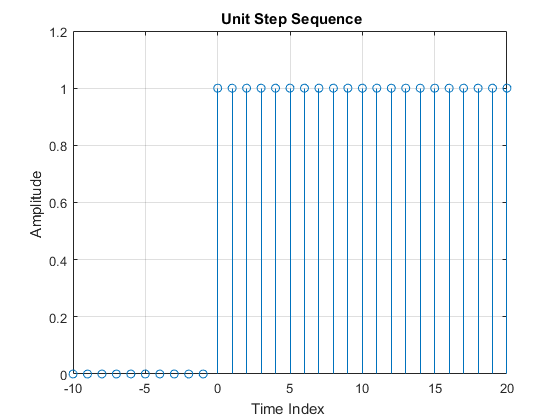
24 - پاسخ ضربه و پاسخ پله یک سیستم انتگرال گیر را بدست آورید.
ابتدا یک سیستم بر اساس ورودی های دلخواه تعریف می کنیم.
می دانیم که : 1 - پاسخ ضربه: (مشتق منهای یکم=انتگرال) پاسخ ضربه=پله واحد
2 - پاسخ پله: (مشتق منهای یکم=انتگرال) پاسخ پله=رمپ
25 - سه ثانیه صدای خود را ضبط کرده و در حوزه زمان و فرکانس نمایش دهید.
26 - حاصل کانولوشن دو سیگنال خواسته شده را بدست آورید.
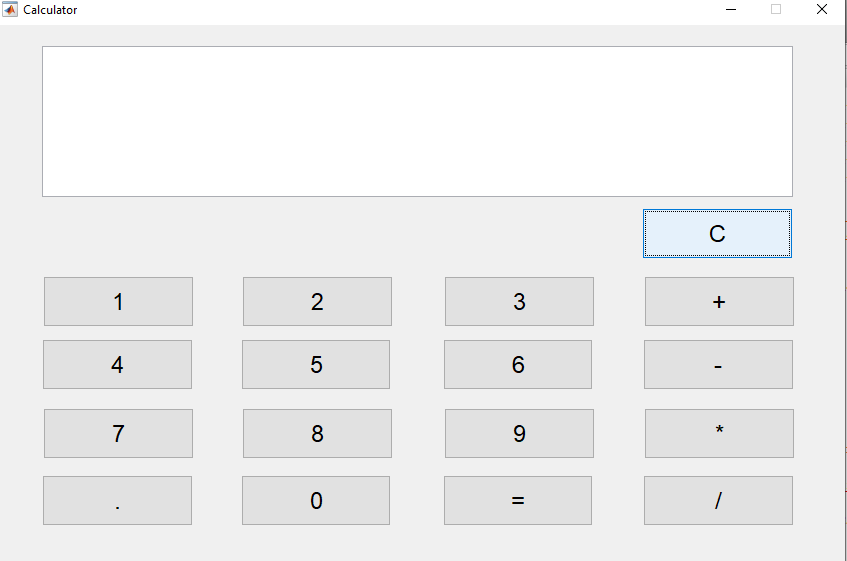
27 - با استفاده از متلب و GUI، ماشین حسابی طراحی کنید که چهار عمل اصلی را انجام دهد. همچنین یک دکمه برای پاک کردن محاسبات داشته باشد.
28 - برنامه ای بنویسید که یک ماتریس از کاربر گرفته و تعداد اعداد مثبت هر ستون را مشخص کند و بجای اعداد منفی در ماتریس به ترتیب شماره ۱و ۲ و... قرار دهد
29 - برنامه ای بنویسید که ریشه های یک چند جمله ای از کاربر گرفته، در صورتی که مجموع ریشه های تابع مثبت بود چند جمله ای را رسم کند اگر مجموع ریشه های چند جمله ای منفی بود مشتق چند جمله ای را رسم کند. اگر مجموع ریشه ها برایر صفر بود چند جمله ای، مشتق و انتگرال آن را در یک شکل رسم کند.
| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.