1 - الگوریتمی بنویسید که فاکتوریل یک عدد را چاپ کند.
2 - الگوریتمی بنویسید که عدد n را از کاربر گرفته و n امین عدد سری فیبوناچی را چاپ کند.
3 - الگوریتمی بنویسید که n امین عدد اول را چاپ کند.
4 - الگوریتم و فلوچارتی رسم کنید که تمام اعداد چهار رقمی که در آن ها حداقل دو رقم یک وجود داشته باشد را نمایش دهد.
5 - الگوریتم و فلوچارتی رسم کنید که کلیه اعداد سه رقمی که حداقل دو رقم آن ها برابر باشند را نمایش دهد.
6 - الگوریتم و فلوچارتی رسم کنید که n عدد را خوانده ، تعیین کند هر کدام چند رقمی هستند ، چند رقم آن ها زوج و چند رقم فرد است.
7 - الگوریتم و فلوچارتی رسم کنید که x و n خوانده ، مجموع n جمله سری زیر را نمایش دهد.
\[ x-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}-...\]
8 - الگوریتم و فلوچارتی رسم کنید که تمام اعداد متقارن 5 رقمی را نمایش دهد.
9 - الگوریتم و فلوچارتی رسم کنید که تعدادی عدد را خوانده ، هر یک از اعداد که بر 9 بخش پذیرند را در خروجی چاپ کند. ( عددی بر 9 بخش پذیر است که مجموع ارقام آن بر 9 بخش پذیر باشد )
10 - الگوریتم و فلوچارتی رسم کنید که x و n را خوانده ، مجموع n جمله سری زیر را چاپ کند.
\[ S=\frac{1}{x}-\frac{1}{x+2x^2}+\frac{1}{x+2x^2+3x^3}-...\]
11 - الگوریتم و فلوچارتی رسم کنید که عددی را خوانده تشخیص دهد این عدد جزء سری فیبوناچی است یا خیر.
12 - الگوریتم و فلوچارتی رسم کنید که عدد صحیح و مثبت n را از ورودی خوانده ، آن را به مبنای دو تبدیل کند و خروجی بنویسید.
13 - الگوریتم و فلوچارتی رسم کنید که یک عدد را به مبنای دو از ورودی خوانده ، آن را به مبنای 10 تبدیل کرده و در خروجی نمایش دهد.
14 - الگوریتمس بنویسید که عدد طبیعی N و حقیقی x را سوال نموده و مقادیر زیر را محاسبه کند.
\[ \begin{matrix}P=\frac{1}{3}+\frac{1}{6}+\frac{1}{9}+...+\frac{1}{N}\\S=1+x+x^2+x^3+...+x^n\\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}+...+\frac{x^{2N-1}}{(2N-1)!}\\T=1\times 2+2 \times 3+...+N \times (N-1)\end{matrix}\]
15 - الگوریتمی بنویسید که تمام اعداد اول کوچکتر از 1000 را تولید نماید.
16 - الگوریتمی بنویسید که بدون استفاده از متغییر سومی محتوبات دو متغییر را جابجا کند.
17 - الگوریتمی بنویسید که عدد طبیعی N را به عنوان ورودی گرفته و معین کند آیا عدد بر مجموع ارقامش بخش پذیر است یا نه؟
18 - الگوریتمی بنویسید که عدد طبیعی N را دریافت کرده و معین کند که چند رقم آن زوج ، چند رقم فرد و چند رقم برابر صفر است.
20 - فلوچارتی بکشید که دو عدد را به عنوان طول و عرض یک مستطیل گرفته و محیط آن را محاسبه و چاپ کند.
21 - فلوچارتی بکشید که یک عدد را گرفته ( فرض بر این است که عدد ورودی صحیح و مثبت است ) و مجموع چهار عدد بعد از آن را چاپ کند. برای مثال عدد ورودی 8 باشد ، این فلوچارت باید حاصل 12+11+10+9 را چاپ کند.
22 - فلوچارتی بکشید که دو عدد صحیح و مثبت را گرفته ( فرض بر این است که عدد اول کوچکتر از عدد دوم است ) ، آنگاه جملاتی از دنباله فیبوناچی که بین این دو عدد قرار دارند را چاپ کند.
23 - فلوچارتی بکشید که طول یک بازه زمانی را بر حسب ثانیه گرفته و آن را برحسب ساعت ، دقیقه و ثانیه چاپ کند. برای مثال 4537 ثانیه را گرفته و 1 و 15 و37 را چاپ کند.
24 - فلوچارتی بکشید که یک عدد را گرفته و 5 عدد اول بعد از آن را چاپ کند.
25 - فلوچارتی بکشید که 10 عدد را گرفته و تعداد اعدادی که از میانگین اعداد ورودی بزرگتر هستند را چاپ کند.
26 - فلوچارتی بکشید که یک عدد را گرفته و اگر در عدد ورودی رقم 3 وجود دارد به جای آن 5 جایگزین کند. برای مثال 237631 را گرفته و 257651 را چاپ کند.
27 - الگوریتمی بنویسید که 2 عدد را از ورودی بگیرد و عدد بزرگتر را در خروجی چاپ کند.
28 - الگوریتمی بنویسید که 10 عدد را از ورودی دریافت کند و بزرگترین عدد را چاپ کند.
29 - الگوریتمی بنویسید که 10 عدد را از ورودی دریافت کند و مجموع آن ها را چاپ کند.
30 - الگوریتمی بنویسید که 10 عدد را از ورودی دریافت کند و مجموع اعداد مثبت آن ها را چاپ کند.
31 - الگوریتمی بنویسید که عددی را دریافت کرده و فاکتوریل آن را حساب کند.
32 - الگوریتمی بنویسید که عدد n و k را دریافت کرده و حاصل عبارت زیر را محاسبه کند .( انتخاب k از n )
\[ \begin{pmatrix} n\\k\end{pmatrix}\]
33 - الگوریتمی بنویسید که آرایه ای ۱۵ عنصری از اعداد صحیح و مثبت از کاربر دریافت کنید که کاملا غیر ترتیبی هستند و بزرگترین و کوچکترین عنصر آن به همراه تعداد اعداد اول ، تعداد تام ، تعداد زوج و فرد و تعداد مضرب ۷ را در آن جداگانه مشخص نمایید و توابع اول و تام را حتما بنویسید.
34 - الگوریتم و فلوچارتی بنویسید که سه عدد a , b , c را که اضلاع یک مثلث هستند را دریافت و مشخص کند که می توان با آن یک مثلث قائم الزاویه تشکیل داد؟
35 - الگوریتم و فلوچارتی بنویسید که عددی را دریافت کند و مشخص کند که آن عدد کامل است یا خیر؟
36 - الگوریتم و فلوچارتی بنویسید که یک عدد در مبنای b را دریافت کرده و آن را به مبنای 10 ببرد.
37 - الگوریتم و فلوچارتی بنویسید که زمان را برحسب ثانیه دریافت کند و مشخص کند که از چند ساعت و چند دقیقه و چند ثانیه تشکیل شده است.
38 - با استفاده از نرم افزار Raptor فلوچارتی رسم کنید که ، تاریخ امروز را به فرمت روز ، ماه و سال را از ورودی دریافت کند و سپس تاریخ روز بعد را به شکل روز ، ماه و سال در خروجی چاپ کند.
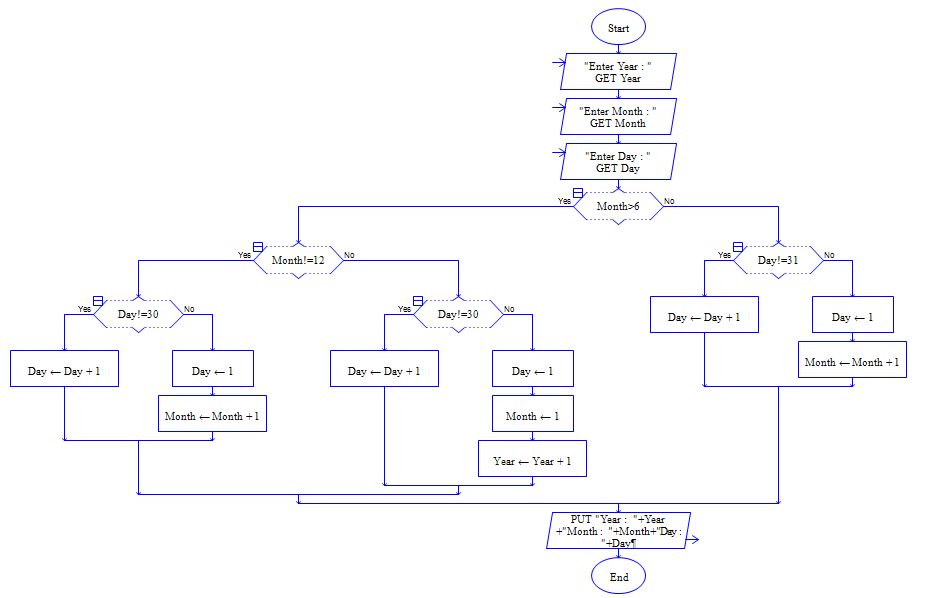
39 - با استفاده از نرم افزار Raptor فلوچارتی رسم کنید که ، n عدد از ورودی بگیرد ، سپس تعداد اول را در خروچی چاپ کند.
40 - با استفاده از نرم افزار Raptor فلوچارتی رسم کنید که ، n عدد از ورودی بخواند سپس فاکتوریل آن ها را در خروجی چاپ کند.
41 - الگوریتمی بنویسید که یک عدد صحیح مثبت شش رقمی را می خواند. اگر عدد زوج است، ارقام آن را جمع می کند. درغیر این صورت، ارقام جداگانه را در همضرب کرده و نتیجه را چاپ نماید.
42 - به یک عدد سه گانه گفته می شود اگر دو برابر و سه برابر عدد شامل تمام ارقام جداگانه بدون تکرار هیچکدام باشند. به عنوان مثال 192که دو برابرش384و سه برابرش576هستند و327 که دو برابرش654 و سه برابرش981هستند سه گانه اند. الگوریتمی بنویسید که همه ی اعداد سه گانه یکم تر از 10000 رانمایش داده و چاپ کند.
43 - الگوریتمی بنویسید که جمله ی اول یک تصاعد هندسی(a)، قدر نسبت تصاعد(q) و شماره ی جمله(n) را خوانده و سپس جمله ی n ام آن را با استفاده از رابطهی 𝑠 = 𝑎𝑞 𝑛−1 محاسبه می کند.
44 - الگوریتمی بنویسید که عدد صحیح n را خوانده و در صورتی که 𝑛 ≤ 1000، مضارب n تا 1000 را چاپ می نماید.
45 - الگوریتمی بنویسید که عدد صحیح n را خوانده و مربع کلیه ی اعداد فرد بین 1 تا n و مکعب کلیه ی اعداد زوج همین بازه را محاسبه نموده و مجموع این دو را چاپ می نماید.
46 - الگوریتمی بنویسید که n عدد را خوانده و مشخص کند چه تعداد از این اعداد مثبت، چه تعداد منفی و چه تعداد برابر صفرند.
47 - فرض کنید از یک دستگاه فروش اتوماتیک تنقلات می توان یک آدامس به قیمت هر عدد برابر 1000 تومان خریداری کرد. همراه با هر آدامس یک قبض تخفیف وجود دارد. با صرف هر 7 قبض تخفیف می توان یک آدامس از دستگاه بازخرید کرد. در این الگوریتم می خواهیم محاسبه کنیم با فرض در اختیار داشتن n تومان و با احتساب امتیازات صرف شده با قبوض تخفیف، حداکثر چه تعداد آدامس با n تومان می توان خریداری کرد؟
مثال: اگر شما 20000 تومان داشته باشید، می توانید ابتدا 20 آدامس خریداری کنید و دارای 20 قبض تخفیف شوید. سپس می توانید به ازای 14 قبض تخفیف دو آدامس اضافی به دست آورید. این دو آدامس اضافه خود 2 قبض تخفیف دیگر برای شما در پی خواهند داشت. بنابراین شما اکنون مجموعا 8 قبض تخفیف دارید. این 8 قبض خود امکان بازخرید کردن یک آدامس دیگر را به شما خواهند داد. در نتیجه شما در نهایت 23 آدامسو دو قبض تخفیف باقی مانده دارید.
الگوریتمی بنویسید که مقدار n تومان را بگیرد و محاسبه کند پس از صرف تمام پولی که در اختیار دارید و صرف کردن بیش ترین تعداد ممکن از قبض های تخفیف جهت بازخرید آدامس های اضافه، در مجموع چه تعداد آدامس می توان جمع آوری کرد. همچنین الگوریتم شما باید به عنوان خروجی تعداد قبض های تخفیف باقی مانده را چاپ کند. این الگوریتم را به گونه ای طراحی کنید که تا زمانی که کاربر اعلام توقف نکرده است بتواند برای مقادیر مختلف ورودی n، خروجی مطلوب را بگیرد.
48 - دستور uptime در سیستم عامل UNIX تعداد روزها، ساعات و دقایق سپری شده از وقتی که آخرین بار سیستم عامل روشن شده بود را نمایش می دهد. به عنوان مثال این دستور ممکن است چاپ کند UP 53 days 12:39. الگوریتمی بنویسید که معادل x روز و yساعت و z ثانیه را به تعداد ثانیه ها که از آخرین باری که سیستم خاموش بودچاپ می کند.
49 - یک عدد متقارن عددیست که از سمت چپ به راست و راست به چپ یکنواخت خوانده می شود. مثلا عدد صحیح 121 متقارن است اما 123چنین نیست. الگوریتمی بنویسید که یک عدد صحیح مثبت حداکثر پنج رقمی ، را خوانده و معین می کند که این عدد متقارن هست یا خیر. اگر کاربر یک عدد صحیح که بین 1 تا پنج رقم باشد وارد نکند الگوریتم شما باید یک پیام خطا چاپ کند.
50 - پزشکان تخمین می زنند که مصرف تقریبا 10 گرم کافئین به طور یک جا مصرف دارویی بیش از حد لزوم و کشنده است. الگوریتمی بنویسید که تعداد میلی گرم کافئین در یک نوشیدنی را دریافت نموده و درخروجی نشان می دهد چه تعداد از آن نوشیدنی ها منجر به مرگ یک شخص خواهد شد. یک اونس معادل 28.35 گرم است. یک قوطی 12 اونسی کولا تقریبا 34 میلی گرم کافئین دارد، در حالی که یک جام قهوه ی 16 اونسی تقریبا 160 میلی گرم کافئین دارد.
جهت سفارش پروژه ، تکلیف و آموزش الگوریتم و فلوچارت ، مبانی برنامه نویسی لطفا با متلب خونه تماس بگیرید، تا پس از بررسی هزینه خدمت شما اعلام گردد.
پشتیبانی ( تلفن ثابت دفتر متلب خونه ) : 02191307193
تلگرام و ایتا : 09364847193