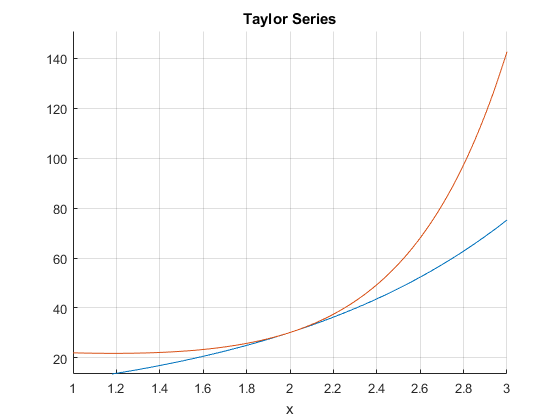
سری تیلور :: مرجع تخصصی برنامه نویسی محاسباتی

تکالیف متلب MATLAB - سری تیلور تابع مختلط ( کد Mat0091 )

1 - تابع زیر را با n جمله نخست بسط تیلور این تابع حول صفر تقریب می زنیم. منحنی های تقریب زده شده را برای n=2,5,10,20 رسم کنید.

\[\begin{matrix} e^{z}\\ ln(z)\\ z^{2}+z \end{matrix}\]

2 - برنامه ای بنویسید که انتگرال معین تابع زیر را در یک بازه دلخواه با روش مستطیلی تخمین بزند. آرگومان های ورودی عبارتند از ابتدای بازه ، انتهای بازه ، و عرض مستطیل

\[\int_{a}^{b} x^{2}-3x+1\]

3 - مقدار عبارت زیر را با استفاده از فرمول تیلور تقریب بزنید.

\[ \sqrt[3]{7}\]

4 - با استفاده از فرمول مک لورن مقدار عبارت زیر را با چهار رقم اعشار درست محاسبه کنید.

\[ sin(10^\circ )\]

5 - با استفاده از سه جمله اول سری مک لورن تابع زیر را تقریب بزنید.

\[ cos(0.5 )\]

6 - نشان دهید برای هر x و y حقیقی رابطه زیر برقرار است.

\[ \left| sin(x)-sin(y)\right|\leq \left|x-y \right|\]

7 - برای سرشکنی کمترین مربعات معمولی y=3x²+2x+10 اگر

\[ x_{i}=\begin{bmatrix}1\\...\\...\\...\\10\end{bmatrix}\]

y را بدست آورید و y ها را خطا دار کرده (randn)

x رو از 1 تا 10 تغییر بده و y ها را به ازای این مقادیر از x بدست بیاورید و سپس y ها را خطا دار کنید.

\[y_{i}+randn\]

خطا دار که شد از

\[x=(A^{T}A)^{-1}A^{T}y\]

استفاده کنید و ببینید به مجهولات که 2 ، 3 و 10 هستند چقدر نزدیک هستید.

8 - تعداد دنباله های دودویی به طول n که دقیقا m بار در آن ها 01 ظاهر شده است را بیابید. n>m

9 - فرض کنید که

الف ) نمایش این عدد را در یک سیستم اعشاری معمولی 4 رقم اعشاری بنویسید.

ب ) گرد شده این عدد را در نمایش علمی 4 رقم اعشاری بنویسید.

ج ) نمایش این عدد را در یک سیستم رایانه ای 4 رقمی بنویسید.

10 - به چهار روش ( استقرا - برهان خلف - مستقیم - contraposition ) رابطه ی زیر را اثبات کنید.

\[1+2+3+4+...+n=\frac{n(n+1)}{2}\]

11 - با استفاده از روش تکراری ژاکوبی جواب دستگاه معادلات زیر را به دست آورید. جواب اولیه را بردار صفر در نظر بگیرید و محاسبات را با 4D انجام دهید.

\[\begin{matrix}4x_{1}-x_{2}+x_{3}=4\\x_{1}+6x_{2}+2x_{3}=9\\-x_{1}-2x_{2}+5x_{3}=2\end{matrix}\]

12 -

13 -

14 -

15 -

16 -

17 -

18 -

19 -

20 -

جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

تکالیف متلب MATLAB - سری تیلور ( کد Mat0063 )

1 - برنامه نویسی محاسبه سری تیلور Taylor برای تابع دلخواه f(x) در نقطه x₀ محاسبه و رسم نماید.

\[f(x)=P_{n}(x)+R_{n}(x)\]

سری تیلور Taylor برایر

\[P_{n}(x)=f(x_{0})+(x-x_{0})f'(x_{0})+ \frac {(x-x_{0})^{2}}{2!}f''(x_{0})+...+\frac {(x-x_{0})^{n}}{n!}f^{n}(x_{0})\]

خطای سری تیلور Taylor برابر است با

\[R_{n}(x)=\frac {(x-x_{0})^{n+1}}{(n+1)!}f^{n+1}(\xi (x))\]

2 - تعداد و حدود تقریبی ریشه معادلات زیر را با روش ترسیمی بدست آورید.

\[x^{2}sin(x)=1\]
\[3xe^{x}-1=0\]
\[e^{x}cos(x)=sin(x)\]
\[2^{x}-x^{2}=0\]
\[x-tan(x)=0\]
\[(x+1)cos(x)=xsin(x)\]

3 - تقریبی از ریشه معادلات زیر را به روش دوبخشی طوری بدست آورید که شرایط زیر بر قرار باشد.

\[x-cos(x)=0 \; \;\;\;\;\;\; \epsilon =10^{-3}\;\;\;\; [0,1]\]

\[x^{2}+x-1=0 \; \;\;\;\;\;\; \epsilon =10^{-2}\;\;\;\; [0,1]\]
\[sin(x)- \frac{x}{2}=0 \; \;\;\;\;\;\; \epsilon =10^{-2}\;\;\;\; [1,2]\]

4 - با نرم افزار متلب نشان دهید که هرچه تعداد جملات استفاده شده در سری تیلور تابع زیر در حول نقطه صفر بیشتر باشد ، تقریب مورد استفاده بسیار بهتر است.

\[ e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+...\]

5 - روش حذفی گاوس در حل سه معادله سه مجهول زیر را با دستورات متلب پیاده سازی کنید.

\[ \left\{\begin{matrix}x+y+z=3 \\2x+5y-4z=3 \\3x+6y-z=8\end{matrix}\right.\]

6 -

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.