1 - مدارات زیر را در محیط سیمولینک Simulink شبیه سازی کنید.
2 - پاسخ پله یک مدار RLC سری را در سیمولینک Simulink شبیه سازی کنید و ولتاژ دو سر مقاومت، خازن و سلف را به همراه جریان مدار نمایش دهید.
3 - با استفاده از سیمولینک Simulink یک فیلتر بالا گذر RC ایجاد کنید
جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.
1 - مطلوبست تابع زیر را در سیمولینک Simulink متلب پیاده سازی نمایید.
\[f=x^{3}+x^{2}-3x-2\]
2 - مطلوبست معادله زیر را در بازه مشخص شده در فضای سیمولینک رسم کنید.
\[f=2x^{3}-4x^{2}+6x \;\;\; \; \; x\in [-5,5] \;\;\; y\in [-100,100]\]
3 - مطلوبست توابع زیر را در سیمولینک پیاده سازی نمایید و خروجی را مشاهده کنید.
\[\begin{matrix} f=5x^{6}+4x^{8}+3x^{2}+6\\ f=e^{x}+15x^{3}+12x\\ f=6log_{10}(x)+7x^{3}+6x+2\\ f=log_{10}(x)-2e^{x}-5x\\ f=2x^{3}-4x^{2}+6x \end{matrix}\]
4 - از یک پالس ، مشتق و انتگرال گرفته و روی اسکوپ به همراه سیگنال اصلی نمایش دهید.
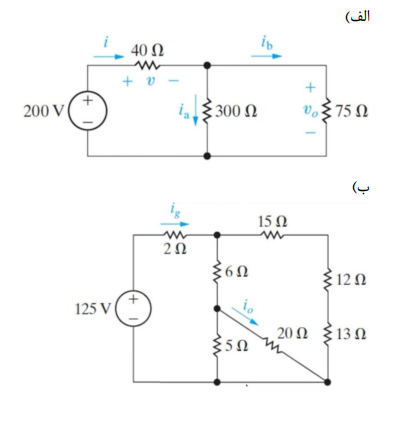
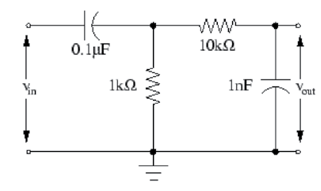
5 - مدار مقابل را در سیمولینک پیاده سازی نمایید. منبع سینوسی با دامنه 4 و فرکانس 6 هرتز است.
6 - معادله غیرخطی زیر را حل کنید
\[-x^{3}-sin(2x)-xcos(x)+5e^{x-1}-3=0\]
7 - دستگاه معادلات زیر را در محیط سیمولینک حل کنید
\[\left\{\begin{matrix} x_{1}+2x_{2}+3x_{3}=3\\ -7x_{1}+5x_{2}+x_{3}=2\\ -3x_{1}+4x_{2}+4x_{3}=1 \end{matrix}\right.\]
8 - تابع تبدیل سیستم زیر را تعریف کنید.
\[G(s)= \frac{Y(s)}{U(s)}=\frac{4s+3}{s^{2}+6s+5}\]
9 - پاسخ ضربه سیستم زیر را بدست آورید.
\[T(s)=\frac{130}{s^{2}+15s+130}\]
\[T(s)=\frac{0.045}{s^{2}+0.025s+0.045}\]
10 - برای سیستم فیدبک واحد نشان داده شده ، پاسخ پله حلقه بسته آن و پایداری را تعیین نمایید.
\[G(s)=\frac{30(s^{2}-5s+3)}{(s+1)(s+2)(s+4)(s+5)}\]
11 - برای سیستم هایی که توابع تبدیل حلقه باز زیر پاسخ پله حلقه بسته را بیابید.
\[G(s)=\frac{3s+2}{2s^{3}+4s^{2}+5s+1}\]
\[G(s)=\frac{50(s+1)}{s(s+3)(s+5)}\]
12 - می خواهیم پاسخ پله و پاسخ ضربه سیستم توصیف شده با تابع تبدیل زیر را بدست آوریم
\[G(s)=\frac{1}{2s^{3}+3s^{2}+s+1}\]
13 - پاسخ حلقه بسته ( با فیدبک واحد منفی ) تابع تبدیل بیان شده در مثال قبل را بدست آورید.
\[G(s)=\frac{1}{2s^{3}+3s^{2}+s+1}\]
14 - اگر برداری به صورت زیر را داشته باشیم ، تبدیل فوریه ی این بردار را محاسبه کنید.
\[x=[1 2 4 8 10]\]
15 - تابعی گسسته را با مقادیر زیر را در نظر بگیرید . تبدیل فوریه گسسته این تابع را حساب کنید.
\[x[0]=1\;\;x[1]=3\;\;x[2]=5\;\;x[3]=7\;\;\]
16 - از طریق محاسبه ی معکوس فوریه ی گسسته یعنی x[m] ، تابع x[n] را بدست آورید.
\[X_{m}=[16 \;\; -4+4j\;\; -4\;\;-4\;\;-4j ]\]
جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.
