1 - پروژه انتگرال گیری عددی : پروژه باید به صورت یک واحد برنامه واحد باشد که با 7 روش زیر انتگرال را در بازه خاص با هر 7 روش محاسبه و چاپ کند.

استفاده از توابع برای هر روش اجباری می باشد.

روش ها : مستطیلی ، ذوزنقه ای ، سیمپسون ، نقطه میانی ، رامبرگ ،گاوس دو نقطه ای و گاوس سه نقطه ای

2 - پروژه محاسبه ریشه های چند جمله ای : ریشه های چند جملهای را محاسبه و چاپ کنید.

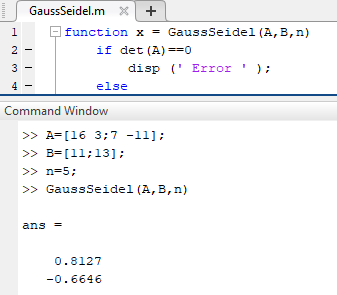
3 - پروژه دستگاه های خطی : یک ماتریس با ابعاد n*n+1 را دریافت کرده و حاصل دستگاه را با 4 روش زیر محاسبه کند.  برای هر روش برنامه جداگانه بنویسید.

روش ها : گاوس ، گاوس جردن ، گاوس پاشنه گری و تجزیه LU

4 - پروژه حل معادلات غیرخطی - برای یک معادلهغیرخطی که از قبل در برنامه وجود دارد ، باید با استفاده از 5 روش و با دریافت بازه مربوطه و دقت محاسبه ، صفرهای آن را محاسبه کند.

استفاده از توابع برای هر روش اجباری می باشد.

روش ها : تصنیف ، خطا و تصحیح ، نقطه ثابت ، نیوتن و وتری

5 - پروژه محاسبه وارون ماتریس : یک ماتریس n*n را گرفته و وارون آن را محاسبه و چاپ کند.

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - قاعده کرامر روشی صریحی برای حل دستگاه معادلات خطی ای که تعداد معادلات با تعداد مجهولات برابر و دستگاه جواب منحصر بفرد دارد، است. این روش از دترمینان‌های ماتریس (مربع) ضرایب و ماتریس‌هایی که از جایگزینی یکی از ستون‌های ماتریس ضرایب با بردار سمت راست معادله بدست می‌آید، تعریف می‌گردد. 

( کد نوشته شده ابتدا با دریافت دو ماتریس A ( باابعاد دلخواه  n*n ) و B ، مقدار x را محاسبه می کند.)

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - روش گاوس سایدل در جبر خطی عددی روش تکراری است که برای حل دستگاه معادلات خطی استفاده می‌شود. 

اگرچه از این روش می‌توان در هر ماتریسی که دارای درایه قطری صفر نباشد استفاده کرد، اما فقط در صورتی همگرایی تضمین می‌شود که ماتریس مثبت معین یا قطری‌غالب باشد.

( کد نوشته شده ابتدا با دریافت دو ماتریس A و B و تعداد تکرار n ، مقدار x را در مرتبه n تکرار محاسبه می کند.

2 - به روش های ژاکوبی و گاوس سیدل جواب دستگاه زیر را بدست آورید.

\[\left\{\begin{matrix} x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=1\\ x_{1}+2x_{2}+3x_{3}+4x_{4}+5x_{5}=0\\ x_{1}+3x_{2}+6x_{3}+10x_{4}+15x_{5}=0\\ x_{1}+4x_{2}+10x_{3}+20x_{4}+35x_{5}=0\\ x_{1}+5x_{2}+15x_{3}+35x_{4}+70x_{5}=0 \end{matrix}\right.\]

نکته مهم در این سوال چک کردن شرط همگرایی روش گاوس سیدل است.

روش گوس سایدل همگرا است، اگر:

الف - ماتریس ضرایب  یک ماتریس مثبت معین متقارن باشد،

ب - ماتریس ضرایب  اکیداً غالب قطری باشد.

ماتریس ضرایب این دستگاه هیچ کدام از دو شرط بالا را ندارد. پس روش گاوس سیدل همگرا نشده و جواب نمی دهد و فقط می توان از روش ژاکوبی استفاده کرد.

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - بسط لاپلاس (یا بسط همسازه‌ای ) برای محاسبه‌ی دترمینان ماتریس مرتبه‌ی n به فرم زیر است

\[\left | A \right |=\sum_{j=1}^{n}(-1)^{i+j} a_{ij} \left | A_{ij} \right |\]

که بسط بر اساس سطر دلخواه i  صورت گرفته است. منظور از Aij (ماتریس کهاد) ماتریسی است که از حذف سطر i ام و ستون j ام ماتریس اصلی به دست آمده است.

( کد نوشته شده می تواند دترمینان هر ماتریس مربعی ( بدون محدودیت در ابعاد را محاسبه کند. ) )

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - در درس محاسبات عددی بیان شد که روش های تخمین ریشه معادلات غیرخطی به دو دسته روش های محصورکننده ریشه  bracketing methods و روشهای باز  open methods تقسیم می گردند. روش های محصور کننده رسیدن به حداقل یک ریشه معادله را در بازه مورد بررسی تضمین می نمایند، ولی نقطه ضعف اساسی آنها روند همگرایی کند در رسیدن به تخمین ریشه با دقت از پیش تعیین شده است. از سوی دیگر، روش های باز دستیابی به ریشه را تضمین نمی نمایند، اما در صورت همگرایی به ریشه، روند همگرایی آنها معمولا سریع و فوق خطی می باشد.

در طول تاریخ علوم محاسباتی، محققان متعددی سعی نمودند با ترکیب روش های فوق از مزایای هر یک از این روش ها در الگوریتم پیشنهادی خود بهره مند شوند. به عبارت دیگر، روش های ترکیبی متعددی در محاسبات عددی ابداع شده اند که هدف آن ها دستیابی تضمین شده به ریشه با یک روند همگرایی سریع است. در زیر یکی از این روش ها که ترکیبی از روش تنصیف  bisection و روش سکانت  secant  می باشد، شرح داده شده است.

مانند روش تنصیف، این روش در شروع نیازمند یک بازه [a,b] به گونهای است که داشته باشیم:

\[f(a)\geq 0\; \;, \; f(b)\leq 0\]

بدین ترتیب تضمین می شود که تابع پیوسته f شامل حداقل یک ریشه در بازه فوق خواهد بود.

تمرین :  تعیین ریشه معادله جبری زیر با دقت خواسته شده . بازه اولیه مورد نیاز برای شروع حل را [3,0] درنظر بگیرید.

\[f(x)=-x^{4}+3x^{2}+2=0\]

2 - تابعی بنویسید که اسم آن Harmonic و ورودی آن N باشد و خروجی آن مقدار سری هارمونی تا جمله‌ی N  باشد. همچنین این تابع نمودار مجموع جزیی را هم رسم کند (یعنی روی محور افقی مقادیر از 1 تا N و به ازای هر مقدار، مجموع جزیی سری هارمونی تا آن مقدار رسم شود.)

3 - بردار سرعت جسمی به جرم 20kg به صورت زیر داده شده است. اگر بازهزمانی برابر 2s باشد ، مطلوبست رسم نمودار نیرو - زمان و شتاب زمان را رسم کنید.

\[V=[0 \; \; 3\; \;6 \; \;9 \; \;10\; \; 9.5 \; \;8 \; \;5 \; \;4 \; \;3 \; \;2\; \; 1.5 \; \;1]\]

| جهت سفارش پروژه و تکلیف پردازش تصویر OpenCV و متلب MATLAB لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.