1 - روش گاوس سایدل در جبر خطی عددی روش تکراری است که برای حل دستگاه معادلات خطی استفاده می‌شود. 

اگرچه از این روش می‌توان در هر ماتریسی که دارای درایه قطری صفر نباشد استفاده کرد، اما فقط در صورتی همگرایی تضمین می‌شود که ماتریس مثبت معین یا قطری‌غالب باشد.

( کد نوشته شده ابتدا با دریافت دو ماتریس A و B و تعداد تکرار n ، مقدار x را در مرتبه n تکرار محاسبه می کند.

2 - به روش های ژاکوبی و گاوس سیدل جواب دستگاه زیر را بدست آورید.

\[\left\{\begin{matrix} x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=1\\ x_{1}+2x_{2}+3x_{3}+4x_{4}+5x_{5}=0\\ x_{1}+3x_{2}+6x_{3}+10x_{4}+15x_{5}=0\\ x_{1}+4x_{2}+10x_{3}+20x_{4}+35x_{5}=0\\ x_{1}+5x_{2}+15x_{3}+35x_{4}+70x_{5}=0 \end{matrix}\right.\]

نکته مهم در این سوال چک کردن شرط همگرایی روش گاوس سیدل است.

روش گوس سایدل همگرا است، اگر:

الف - ماتریس ضرایب  یک ماتریس مثبت معین متقارن باشد،

ب - ماتریس ضرایب  اکیداً غالب قطری باشد.

ماتریس ضرایب این دستگاه هیچ کدام از دو شرط بالا را ندارد. پس روش گاوس سیدل همگرا نشده و جواب نمی دهد و فقط می توان از روش ژاکوبی استفاده کرد.

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - بسط لاپلاس (یا بسط همسازه‌ای ) برای محاسبه‌ی دترمینان ماتریس مرتبه‌ی n به فرم زیر است

\[\left | A \right |=\sum_{j=1}^{n}(-1)^{i+j} a_{ij} \left | A_{ij} \right |\]

که بسط بر اساس سطر دلخواه i  صورت گرفته است. منظور از Aij (ماتریس کهاد) ماتریسی است که از حذف سطر i ام و ستون j ام ماتریس اصلی به دست آمده است.

( کد نوشته شده می تواند دترمینان هر ماتریس مربعی ( بدون محدودیت در ابعاد را محاسبه کند. ) )

| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

حل مسائل کتاب Chemical and Biomedical Engineering Calculations Using Python

1 - You have been hired by a specialty chemical company that has been researching the physical properties of acetone (a common chemical for removing nail polish). The company observed that at an unknown temperature, acetone exhibited the same heat capacity as water. The company found the following quadratic equation for the heat capacity of acetone as a function of temperature

\[C_{p}=26.63+0.183T-45.86\times 10^{-6}T^{2} \; \; \; \; J/(mol.K)\]

You have been hired to determine the temperature at which acetone has the same heat capacity as water (assume that water has a constant heat capacity of 75.6 J/(mol ⋅ K)) on a per mol basis. Finally, the company has two additional requirements:

(1) you need to determine an equation for the change in heat capacity as a function of temperature, that is, dCp dT , and

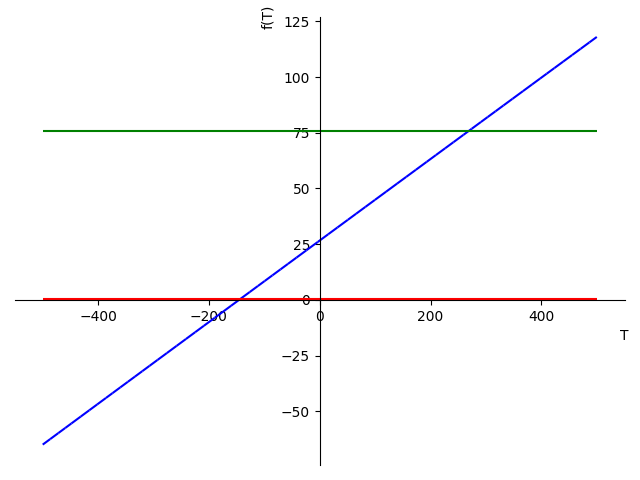
(2) plot the heat capacity as a function of temperature over the full range of temperatures where the heat capacity of acetone might equal the constant head capacity of water. The company is notoriously skeptical of people that perform mathematical analysis “by hand” and is requiring that you perform all calculations using symbolic mathematics software.

2 -You have been hired by the recently reformed La Vie Claire cycling team (this is the team that Greg LeMond won the Tour de France with in 1986 – see the ESPN 30 for 30 documentary, “Slaying the Badger”). The new team manager knows a little physics and made an interesting observation while studying the standard fluid dynamics equation describing the drag force on a body moving through air (or any Newtonian fluid):

\[F_{D}=C_{D}A\frac{\rho V^{2}}{2.0}\]

where FD, the drag force, is approximately equal to the force the rider is applying to the pedals (neglecting mechanical resistance) when riding on a flat surface. The team manager claimed that for a given force from the rider, the equation should have two solutions for the velocity, V, because it is quadratic. The manager further asserted that if riders could change their velocity somehow, they could shift their velocity to the other, faster solution to the equation without having to change the force on the pedals. You have been hired by the team owner to investigate this claim. Using symbolic mathematics software, show that there is only one positive velocity solution to the equation if FD, the force, CDA (the drag coefficient multiplied by the rider’s frontal or cross-sectional area), and 𝜌 (the density of air, 1.0 kg∕m3) are all positive. The second half of the owner’s request is that you calculate the cyclist’s velocity (in meters per second and miles per hour) using the following assumptions: • Professional cyclists perform 10,000 kJ/day of work • In a major race, cyclists ride 250,000 m/day • Work is force times distance (i.e., force is work over distance) • CDA for a cyclists alone on the road is 0.7–0.9 m2 Finally, estimate the velocity of the same cyclist in a group where each cyclist can draft off the person in front of them, thus reducing CDA to 0.5–0.7m2.

2 -

3 -

4 -

5 -

6 -

7 -

8 -

9 -

10 -

| جهت سفارش پروژه ، تکلیف و آموزش پروژه های محاسباتی پایتون Python لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - در درس محاسبات عددی بیان شد که روش های تخمین ریشه معادلات غیرخطی به دو دسته روش های محصورکننده ریشه  bracketing methods و روشهای باز  open methods تقسیم می گردند. روش های محصور کننده رسیدن به حداقل یک ریشه معادله را در بازه مورد بررسی تضمین می نمایند، ولی نقطه ضعف اساسی آنها روند همگرایی کند در رسیدن به تخمین ریشه با دقت از پیش تعیین شده است. از سوی دیگر، روش های باز دستیابی به ریشه را تضمین نمی نمایند، اما در صورت همگرایی به ریشه، روند همگرایی آنها معمولا سریع و فوق خطی می باشد.

در طول تاریخ علوم محاسباتی، محققان متعددی سعی نمودند با ترکیب روش های فوق از مزایای هر یک از این روش ها در الگوریتم پیشنهادی خود بهره مند شوند. به عبارت دیگر، روش های ترکیبی متعددی در محاسبات عددی ابداع شده اند که هدف آن ها دستیابی تضمین شده به ریشه با یک روند همگرایی سریع است. در زیر یکی از این روش ها که ترکیبی از روش تنصیف  bisection و روش سکانت  secant  می باشد، شرح داده شده است.

مانند روش تنصیف، این روش در شروع نیازمند یک بازه [a,b] به گونهای است که داشته باشیم:

\[f(a)\geq 0\; \;, \; f(b)\leq 0\]

بدین ترتیب تضمین می شود که تابع پیوسته f شامل حداقل یک ریشه در بازه فوق خواهد بود.

تمرین :  تعیین ریشه معادله جبری زیر با دقت خواسته شده . بازه اولیه مورد نیاز برای شروع حل را [3,0] درنظر بگیرید.

\[f(x)=-x^{4}+3x^{2}+2=0\]

2 - تابعی بنویسید که اسم آن Harmonic و ورودی آن N باشد و خروجی آن مقدار سری هارمونی تا جمله‌ی N  باشد. همچنین این تابع نمودار مجموع جزیی را هم رسم کند (یعنی روی محور افقی مقادیر از 1 تا N و به ازای هر مقدار، مجموع جزیی سری هارمونی تا آن مقدار رسم شود.)

3 - بردار سرعت جسمی به جرم 20kg به صورت زیر داده شده است. اگر بازهزمانی برابر 2s باشد ، مطلوبست رسم نمودار نیرو - زمان و شتاب زمان را رسم کنید.

\[V=[0 \; \; 3\; \;6 \; \;9 \; \;10\; \; 9.5 \; \;8 \; \;5 \; \;4 \; \;3 \; \;2\; \; 1.5 \; \;1]\]

| جهت سفارش پروژه و تکلیف پردازش تصویر OpenCV و متلب MATLAB لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - برنامه ای که یک بردار 100*1 از اعداد تصادفی بین 1 تا 100 دریافت کند ( اعداد اعشاری ) و سپس آن ها را به صورت صعودی مرتب کند. ( اجازه استفاده از دستور sort را ندارید و باید با استفاده از حلقه ها بردار را مرتب کنید )

2 - یک تابع بنویسید که دو چند جمله ای از درجه دلخواه را جمع یا تفریق یا ضرب نمیاد. از p=polyaddsubmult(p1,p2,operation) به عنوان نام تابع استفاده نمایید. دوپارامتر نخست ورودی p1و p2 بردارهای ضرایب دو چند جمله ای می باشند. ( دقت شود که در جکع یا تفریق اگر دو چند جمله ای هم درجه نباشند ، تابع به تعداد کافی عناصر صفر به بردار کوچکتر اضافه کند، اما در ضرب، دو چند جمله ای می توانند از درجه دلخواه باشند. ) پارامتر سوم ورودی operation یک رشته است، که برای جمع یا تفریق و یا ضرب بردارها باید به ترتیب از add یا sub و یا mult استفاده شود. پارامتر خروجی بردار ضریاب چند جمله ای حاصل می باشد.

3 - برنامه مربوط به polyaddsubmult را به گونه ای بنویسید که سه زیرتابع polyadd , polysub و  polymult به ترتیب برای محاسبه جمع دو چند جمله ای ، تفریق دو چند جمله ای و ضرب دو چند جمله ای استفاده نماید.

4 - همچنین برنامه ای را در یک فایل منتی جهت دریاف بردارهای دو چند جمله ای و رشته مورد نظر جهت جمع ، تفریق یا ضرب بردارها operation و در نهایت جهت نمایش خروجی ( حاصل جمع ، یا حاصل تفریق ، یا حاصل ضرب بردارهای مورد نظر ) بنویسید. این برنامه باید به گونه ای نوشته شود که از تابع polyaddsubmult استفاده نماید. نام این فایل متنی را polynomial قرار دهید.

 5 - دستور MATLAB  برای هریک از موارد زیر را بنویسید و برای هر کدام یک مثال بزنید

حل دستگاه خطی

محاسبه دترمینان ماتریس

  محاسبه چند جمله ای مشخصه ماتریس

محاسبه بردارهای ویژه ماتریس

تبدیل یک مجموعه مستقل خطی از بردارها به یک مجموعه متعامد یکه از بردارها با فضای تولید شده یکسان

6 - وقتی نرم افزار متلب MATLAB آغاز می شود ، یک پنجره اصلی باز می شود که تعدادی پنجره های دیگر در آن دیده می شود. نام سه پنجره از آن ها را بنویسید و کارکرد هر یک از آن ها را توضیح دهید.

7 - قوانین و محدودیت های انتخاب اسامی متغییر ها را بنویسید.

* نام متغیر باید از حروف کوچک و بزرگ ، اعداد و علامت _ تشکیل شده باشد

* نام متغییر نمی تواند با عدد یا _ شروع شود و حتما باید با حروف کوچک و بزرگ شروع شود.

* در نام متغییر نمی توان فاصله space گذاشت.

* نمی توان نام متغیر را در دو سطر نوشت.

* از کلمات رزرو شده مانند for  و  if  و ...  و توابع داخلی متلب نمی توان به عنوان متغیر استفاده کرد

* متلب حساس به حروف بزرگ و کوچک می باشد. این گفته، به این معنی است که بین حروف بزرگ و کوچک، تفاوت وجود دارد

* حداقل طول یک متغیر یک کاراکتر و حداکثر طول آن 63 کاراکتر است.

8 - کارکرد هر یک از دستورهای زیر را بنویسید شکل ( یا شکل های ) ممکن برای بکارگیری هریک از آن ها را ( در صورت وجود ) بیان کنید.

الف - whos

9 - چند جمله ای به صورت دلخواه تعریف کرده و ریشه های آن را به صورت یک بردار بدست آورید.

10 - ابتدا برداری متناظر با ریشه های یک چند جمله ای تشکیل داده ، سپس چند مله ای متناظر با آن را پیدا کنید.

11 - تابعی دلخواه 3 متغییره ابتدا بنویسید و سپس بر حسب یکی از متغییر ها مرتب کنید.

12 - کاربر دستورهای expand و  factor را در مثالی دلخواه بررسی کنید.

13 - دستگاه معادلات زیر را با استفاده از دستور solve حل نموده و مجهولات را با استفاده از نرم افزار MATLAB بدست آورید.

14 - ریشه های چند جمله ای زیر را بدست آورید.

15 - چهار نوع داده مختلف و دلخواه در نظر بگیرید.

الف - نمودار هر کدام را به صورت مجزا رسم نمایید.

ب - هر چهار نمودار را در یک شکل رسم نمایید.

ج - شکل را به چهار بخش کرده و در هر کدام یک نمودار را رسم کنید

د - شکل را به شش قسمت تقسیم کنید ، در دو بخش اول آن یک شکل از هر چهار منحنی را رسم کنید و در سایر بخش ها به صورت دو به دو منحنی هار ا مقایسه کنید.

| جهت سفارش پروژه و تکلیف پردازش تصویر OpenCV و متلب MATLAB لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.