1 - مدارات زیر را در محیط سیمولینک  Simulink شبیه سازی کنید.

2 - پاسخ پله یک مدار RLC سری را در سیمولینک Simulink شبیه سازی کنید و ولتاژ دو سر مقاومت، خازن و سلف را به همراه جریان مدار نمایش دهید.

3 - با استفاده از سیمولینک Simulink یک فیلتر بالا گذر RC ایجاد کنید

جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - مطلوبست تابع زیر را در سیمولینک Simulink متلب پیاده سازی نمایید.

\[f=x^{3}+x^{2}-3x-2\]

2 - مطلوبست معادله زیر را در بازه مشخص شده در فضای سیمولینک رسم کنید.

\[f=2x^{3}-4x^{2}+6x \;\;\; \; \; x\in [-5,5] \;\;\; y\in [-100,100]\]

3 - مطلوبست توابع زیر را در سیمولینک پیاده سازی نمایید و خروجی را مشاهده کنید.

\[\begin{matrix} f=5x^{6}+4x^{8}+3x^{2}+6\\ f=e^{x}+15x^{3}+12x\\ f=6log_{10}(x)+7x^{3}+6x+2\\ f=log_{10}(x)-2e^{x}-5x\\ f=2x^{3}-4x^{2}+6x \end{matrix}\]

4 - از یک پالس ، مشتق و انتگرال گرفته و روی اسکوپ به همراه سیگنال اصلی نمایش دهید.

5 - مدار مقابل را در سیمولینک پیاده سازی نمایید. منبع سینوسی با دامنه 4 و فرکانس 6 هرتز است.

6 - معادله غیرخطی زیر را حل کنید 

\[-x^{3}-sin(2x)-xcos(x)+5e^{x-1}-3=0\]

7 - دستگاه معادلات زیر را در محیط سیمولینک حل کنید

\[\left\{\begin{matrix} x_{1}+2x_{2}+3x_{3}=3\\ -7x_{1}+5x_{2}+x_{3}=2\\ -3x_{1}+4x_{2}+4x_{3}=1 \end{matrix}\right.\]

8 - تابع تبدیل سیستم زیر را تعریف کنید.

\[G(s)= \frac{Y(s)}{U(s)}=\frac{4s+3}{s^{2}+6s+5}\]

9 - پاسخ ضربه سیستم زیر را بدست آورید.

\[T(s)=\frac{130}{s^{2}+15s+130}\]

\[T(s)=\frac{0.045}{s^{2}+0.025s+0.045}\]

10 - برای سیستم فیدبک واحد نشان داده شده ، پاسخ پله حلقه بسته آن و پایداری را تعیین نمایید.

\[G(s)=\frac{30(s^{2}-5s+3)}{(s+1)(s+2)(s+4)(s+5)}\]

11 - برای سیستم هایی که توابع تبدیل حلقه باز زیر پاسخ پله حلقه بسته را بیابید.

\[G(s)=\frac{3s+2}{2s^{3}+4s^{2}+5s+1}\]

\[G(s)=\frac{50(s+1)}{s(s+3)(s+5)}\]

12 - می خواهیم پاسخ پله و پاسخ ضربه سیستم توصیف شده با تابع تبدیل زیر را بدست آوریم

\[G(s)=\frac{1}{2s^{3}+3s^{2}+s+1}\]

13 - پاسخ حلقه بسته ( با فیدبک واحد منفی ) تابع تبدیل بیان شده در مثال قبل را بدست آورید.

\[G(s)=\frac{1}{2s^{3}+3s^{2}+s+1}\]

14 - اگر برداری به صورت زیر را داشته باشیم ، تبدیل فوریه ی این بردار را محاسبه کنید.

\[x=[1 2 4 8 10]\]

15 - تابعی گسسته را با مقادیر زیر را در نظر بگیرید . تبدیل فوریه گسسته این تابع را حساب کنید.

\[x[0]=1\;\;x[1]=3\;\;x[2]=5\;\;x[3]=7\;\;\]

16 - از طریق محاسبه ی معکوس فوریه ی گسسته یعنی x[m] ، تابع x[n] را بدست آورید.

\[X_{m}=[16 \;\; -4+4j\;\; -4\;\;-4\;\;-4j ]\]

جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - جریان آب بین دو نقطه A و B جاری است ، به طوری که فرضیات معادله برنولی در این سیستم بر قرار است. برنامه ای بنویسید که با دریافت اطلاعات مربوط به ارتفاع نقاط A و B ( یعنی Za وZb ) ، فشارهای نقاط A و B ( یعنی Pa و Pb ) و همچنینی سرعت نقطه A ( یعنی Va ) ، سرعت نقطه  B ( یعنی Vb ) را بدست آورد. معادله برنولی به صورت زیر است.

\[\frac {P_{A}}{\gamma}+ \frac{V_{A}^{2}}{2g}+Z_{A}=\frac {P_{B}}{\gamma}+ \frac{V_{B}^{2}}{2g}+Z_{B}\]

2 - برنامه ای بنویسید که دو عدد از کاربر گرفته و باقیمانده عدد اول بر عدد دوم را بدست بیاورد.

3 - برنامه ای بنویسید که دو متغیر عددی را از ورودی گرفته و بدون استفاده از متغیر کمکی محتویات آنها را عوض کند.

4 - برنامه ای بنویسید که سه آرایه سه در سه از کاربر بگیرد و آنها را به یک آرایه 3×3×3 تبدیل کند.

5 - برنامه ای بنویسید که یک ماتریس 1111 در 1111 به نحوی تولید کند که عناصر قطر اصلی و فرعی آن عدد 50 و سایر عناصر عدد 100 باشد.

6 - برنامه ای بنویسید که دو آرایه مربعی A و B را از کاربر دریافت کرده و عناصر قطر اصلی A را در عناصر قطر فرعی B ضرب کرده و مجموع این اعداد را در خروجی نشان دهد.

7 - برنامه ای بنویسید که یک بردار با 11 درایه را دریافت کرده و آن را به یک آرایه 11 در 11 تبدیل کند به صورتی که عناصر بردار بر روی قطر اصلی آرایه 11 در 11 قرار بگیرد و سایر عناصر آرایه صفر باشند.

8 - برنامه ای بنویسید که n نمره دریافت کند و معدل آن ها و بزرگترین عدد زیر 10 را چاپ کند. 

9 - برنامه ای بنویسید که n عدد را دریافت کند ، میانگین و واریانس اعداد را چاپ کند.

10 - برنامه ای بنویسید که عدد n را از کاربر بگیرد و مثلث زیر را به طول ضلع n چاپ کند.

11 - برنامه ای بنویسید که n عدد از کاربر دریافت کند و عددی که کمترین مجموع ارقام را دارد، در خروجی نمایش دهد.

مثال : 64  84  367  21  756  45

در بین اعداد بالا 21 کمترین مجموع ارقام را دارد . پس 21 باید در خروجی نمایش داده شود.

12 - برنامه ای بنویسید که یک عدد را گرفته سپس معادل آن در مبنای 2 را چاپ کند.

13 - برنامه ای بنویسید که یک عدد را گرفته سپس معادل آن در مبنای 8 را چاپ کند.

14 - برنامه ای بنویسید که دو عدد در مبنای 8 را گرفته سپس حاصل جمع و ضرب آن ها را محاسبه و چاپ کند.

15 - برنامه ای بنویسید که یک عدد در مبنای  2 را گرفته سپس معادل آن در مبنای 10 را چاپ کند.

16 - برنامه ای بنویسید که یک عدد در مبنای  8 را گرفته سپس معادل آن در مبنای 10 را چاپ کند.

17 - برنامه ای بنویسید که یک عدد در مبنای  2 را گرفته سپس به مبنای 8 ببرد.

18 - برنامه ای بنویسید که یک عدد را گرفته سپس معادل ان در مبنای 16 را چاپ کند.

19 -برنامه ای بنویسید که یک عدد در مبنای 2 را گرفته سپس مستقیما به مبنای 16 ببرد.

20 - برنامه ای بنویسید که برای یک معادله خاص ، x₁ و x₂ را گرفته و مقدار انتگرال آن را از  x₁ تا x₂ را با دقت ^7-10 محاسبه و نتیچه را چاپ کند. ( روش های مستطیلی ، ذوزنقه ای ، سیمپسون و نقطه میانی )

21 - برنامه ای بنویسید که مقدار انتگرال زیر را با دقت 0.0001 محاسبه و چاپ کنید.

\[\int_{1}^{5}\frac{sin(x)}{x}dx\]

22 - برنامه ای بنویسید که برای یک معادله غیرخطی خاص دو عدد x₁ و x₂ را گرفته و ریشه معادله را در این بازه چاپ کند. ( روش های تصنیف ، خطا و تصحیح ، وتری ، نیوتون و نقطه ثابت )

23 - برنامه ای بنویسید که برای یک معادله غیرخطی خاص تمام ریشه های آن را محاسبه و چاپ کند.

24 - برنامه ای بنویسد که دو عدد m و n را گرفته سپس مقدار \[\binom{m}{n}\] را محاسبه و چاپ کند.

25 - برنامه ای بنویسید که عدد n را گرفته سپس سطر n ام از مثلث پاسکال را چاپ کند.

26 - برنامه ای بنویسید که عدد n را گرفته سپس n سطر از مثلث پاسکال را چاپ کند.

27 - برنامه ای بنویسید که یک عدد اعشاری در مبنای 10 را گرفته و معادل آن در مبنای 2 را ( تا 5 رقم اعشار ) چاپ کند.

28 - برنامه ای بنویسید که یک عدد اعشاری در مبنای 10 را گرفته و معادل آن در مبنای 8 را ( تا 5 رقم اعشار ) چاپ کند.

29 - برنامه ای بنویسید که یک عدد اعشاری در مبنای 2 را گرفته و معادل آن در مبنای 10 را ( تا 5 رقم اعشار ) چاپ کند.

30 - برنامه ای بنویسید که یک عدد اعشاری در مبنای 10 را گرفته و معادل آن در مبنای 16 را ( تا 5 رقم اعشار ) چاپ کند.

31 - برنامه ای بنویسید که کلیه اعداد سه رقمی را که بتوان آن ها را به صورت xyz=x³+y³+z³ نوشت را چاپ کند.

32 - جواب سری زیر :

\[ \frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{100}\]

\[ \frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+...+\frac{1}{100!}\]

\[ \frac{1}{20}+\frac{2}{19}+\frac{3}{18}+...+\frac{20}{1}\]

\[ \frac{1}{1!}-\frac{1}{2!}+\frac{1}{3!}+...-\frac{1}{100!}\]

\[ \frac{1}{1!}+\frac{1}{3!}+\frac{1}{5!}+...+\frac{1}{99!}\]

\[1- \frac{1}{2!}+\frac{1}{4!}-\frac{1}{8!}+...+\frac{1}{100!}\]

33 - جواب سری مقابل را با دقت ^7-10 را بدست آورید

\[\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+...\]

34 - برنامه ای بنویسید که مقدار x را گرفته سپس جواب سری مقابل را با دقت ^7-10 را بدست آورید

\[1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+...\]

\[1+\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+...\]
\[1-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}+...\]

\[\frac{1!}{1}+\frac{2!}{2^{2}}+\frac{3!}{3^{3}}+...+\frac{100!}{100^{100}}\]

35 - جواب سری مقابل را با دقت ^7-10 را بدست آورید

\[\frac{1!}{1}+\frac{2!}{2^{2}}+\frac{3!}{3^{3}}+...\]

\[\frac{1!}{1}-\frac{3!}{3^{3}}+\frac{5!}{5^{5}}+...\]

\[1+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{2+...}}}}\]

36 - 35 - جواب سری مقابل را با دقت ^7-10 را بدست آورید

\[ln(x)=2\left [ \left ( \frac{x-1}{x+1} \right )+ \frac{1}{3}\left( \frac{x-1}{x+1} \right )^{3}+ \frac{1}{5} \left( \frac{x-1}{x+1} \right )^{5}+... \right ]\]

37 - سری های مربوط به sin(x) , cos(x) , e^x , ln(x) , ...  را که از بسط تیلور بدست می آیند را پیدا کرده و برنامه ای بنویسید که مقدار x را گرفته و سری مورد نظر را بادقت ^7-10 محاسبه و چاپ کند.

38 - ماتریس یا مربع جادویی (magic) از مرتبه 3<n یک ماتریس n در n است به نحوی که حاصلجمع عناصر هر سطر برابر حاصلجمع عناصر هر ستون و برابر مقداری ثابت است. ماتریس جادویی در نرمافزار متلب با دستور magic ساخته میشود. در مثال زیر حاصلجمع عناصر هر سطر برابر حاصلجمع عناصر هر ستون و برابر با عدد 15 است. حاصلجمع عناصر روی قطــر اصلی نیز برابر حاصلجمع عناصر روی قطر فرعی و برابر عدد 15 می باشد.

الف) برنامه ای بنویسید که ماتریس مربعی A را دریافت نموده سپس نشان دهد آیا ماتریس A خواص ماتریس جادویی را دارد ؟

ب) به غیر از ماتریس magic حداقل دو ماتریس دیگر در متلب خواص جادویی را دارند. آنها را نام ببرید

ج) با استفاده از برنامه نشان دهید تفاضل ماتریس جادویی با ترانهاده خودش یک ماتریس جادویی با عدد صفر می سازد به نحوی که حاصل جمع عناصر هر سطر برابر حاصلجمع عناصر هر ستون و برابر مقدار صفر است. (برنامه را برای ماتریس جادویی از مرتبه 3 الی 1000 امتحان کنید)

د) با چند مثال نشان دهید هر ترکیب خطی ماتریس جادویی با ترانهاده خودش خواص ماتریس جادویی قسمت ج را دارد.

39 - فرض کنید ده دانشجو داریم به نامهای a و b و c و به همین ترتیب تا j . برنامه ای بنویسید که به صورت تصادفی برای هر یک از این دانشجویان نمره ای بین صفر تا بیست ایجاد کند. سپس میانگین نمرات را محاسبه کنید. سپس نمرات به ترتیب از کم به زیاد مرتب کند به طوری که مشخص باشد هر دانشجو در چه رتبهای قرار دارد. سپ س کسانی که نمره کمتر از ده شده اند را مشخص کند.

40 - گر شما $ 1000 در بانکی با نرخ سود ساالنه %12 سپرده گذاری کنید پس از یکسال $1120 خواهید داشت. فرض کنید به جای پرداخت ساالنه سود، پرداخت ماهانه و با نرخ سود ماهانه %1 باشد یک برنامه ای بنویسید که دارایی شما را پس از یکسال محاسبه کنید. سپس تفاوت سود شما پس از تعداد سال مشخص (مثال ده سال) را با نرخ ساالنه و ماهانه بدست آورد . اگر نرخ سود روزانه %033.0 باشد، این تفاوت چقدر خواهد بود؟

41 - برنامه ای بنویسید یک عدد دریافت کند، چک کند اگر عدد دریافتی یک عدد صحیح مثبت نیست پیام با این مضمون چاپ کند که لطفا یک عدد صحیح مثبت وارد کنید. اگر عدد دریافتی صحیح و مثبت بود مثلثی با طول * چاپ کند که در هر ضلع آن به تعداد عدد دریافتی * باشد.

42 - روز اول فروردین دوشنبه است. برنامه ای بنویسید که روز و ماه را دریافت کند. (مثال روز ۲۳ ماه ۷ مهر) را دریافت کند. بررسی کند که عدد ماه حتما یکی از اعداد ۱ تا ۱۲ باشد و مطابق با ماه عدد روز بین ۱ تا ۲۹ یا ۳۰ یا ۳۱ باشد. در غیر این صورت پیام خطا دهد. سپس با داشتن عدد درست روز و ماه بگوید که آن روز چند شنبه است

43 - از روش نیوتن استفاده کنید و یک برنامه بنویسید که معادله  x^3-cos(x) را حل کند.

44 - برنامه ای بنویسید که یک عدد را از اپراتور بگیرد و اعداد کوچکتر از آن که اول نیستند را چاپ کند.

45 - برنامه ای بنویسید که دو ماتریس خطی از اپراتور بگیرد و درایه های مشترک ( یکسان ) آن دو ماتریس را چاپ کند.

46 - برنامه ای بنویسید که دو آرایه از اعداد صحیح و مثبت به طول یکسان را دریافت نموده و سپس تعداد عناصر آن دو آرایه را که در جایگاه یکسان مقادیر یکسان دارند را نشان دهد.

47 - برنامه ای بنویسید که در آن مدار x را از 10 تا 100 بگیرد و مقدار تابع زیر را حساب کند و مقدار خروجی تابع را درون یک بردار قرار دهد.

\[y=5x^{4}-2x^{3}-2x+28\]

48 - تابع ذیل را با یک چند جمله ای درجه 5 تخمین بزنید.

49 - با استفاده  از متلب و دستورات مربوط به چند جمله ای ها حاصل این انتگرال را محاسبه کنید.

\[\int_{-3}^{2}\frac{d^{2}}{dx^{2}}(x^{\alpha +3}-x^{\beta +2}+x^{\gamma +1})(x^{4}-4x^{3}+5)dx\]

50 - توابع ارائه شد در سمت الف و ب را به ترتیب با رنگ آبی و سبز و با کیفیت مناسبی رسم نمایید. سپس در یک نمودار دیگری توابع سمت پ و ت را با کیفیت خوب و به ترتیب با رنگ مشکی و قرمز رسم کنید. پس از آن  در همان نمودار اولی تابع قسمت ث را رسم نمایید. نمودارهای بدست آمده را به صورت یک فایل pdf به پاسخنامه خود پیوست کنید. نمودارهای ارائه شد باید دارای legend و xlabel وylabel با سایز و فونت مناسب باشند. همچنین در صورت نیازی ylim را طوری تنظیم نمایید که تغییرات نمودار بهتر با چشم دید شوند.

| جهت سفارش پروژه ، تکلیف و آموزش نرم افزار متلب MATLAB لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - تابعی بنویسید که دوماتریس A و B را بگیرد و B را در A جستجو کند. در صورتی که B در A موجود بود ، مختصات آن را برگرداند. ( یعنی اندیسی از A که گوشه سمت چپ بالای B در آن قرار دارد ) درغیر این صورت خروجی را صفر برگرداند.

2 - برنامه ای بنویسید که n را بگیرد و مثلث خیام - پاسکال از سطر اول تا n ام را در یک آرایه دو بعدی برگرداند. به جای عناصر تعریف نشده صفر قرار دهد.

3 - با استفاده از روش انتگرال گیری عددی سیمپسون Simpson ، انتگرال دو بعدی زیر رار محاسبه کنید.

\[\int_{0}^{1}\int_{0}^{2}xy^{2}dydx\]

4 - انتگرال تابع زیر را در بازه [0,1] به روش های ذوزنقه و سیمپسون Simpson بدست آورید.

\[f(x)=x^{3}+2x^{2}+x+1\]

5 - تابعی بنویسید که یک چندجمله ای ( به صورت یک بردار سطری ) و یک بردار دو عنصری ( حاوی دامنه ترسیم ) را از کاربر بگیرد و نمودار چند جمله ای را در دامنه مشخص شده ترسیم کند.

6 - برنامه ای بنویسید که دو ماتریس سطری با طول m و n را از ورودی گرفته و یک ماتریس ستونی به طول m+n بسازد که ابتدا عناصر ماتریس n عنصری  و سپس عناصر ماتریس m عنصری در آن ریخته شود.

7 - برنامه ای بنویسید که 10 عدد را از کاربر گرفته و در ماتریس ستونی قرار دهد و سپس با ترتیب بالعکس در یک ماتریس ستونی دیگر ذخیره نماید.

8 - برنامه ای بنویسید که عدد دلخواه A را از کاربر گرفته و قدرمطلق آن را محاسبه کند.

9 - برنامه ای بنویسید که نمره یک دانشجو را دریافت کند، اگر نمره بالای 18 بود چاپ کند عالی، اگر بالای 14بود چاپ کند خوب، اگر بالای 10 بود چاپ کند ضعیف و در غیر این صورت چاپ کند مردود.

10 - برنامه ای بنویسید که با استفاده از حلقه while،توان سوم اعداد یک تا 6 رامحاسبه کند

11 - با استفاده از حلقه for مجموع زیر را محاسبه کنید

\[y=\sum _{i=1}^{n} \frac{1}{\sqrt{i}}\]

12 - سوال قبل را در حالتی بنویسید که n را به عنوان ورودی را از کاربر بگیرد و اگر عدد کوچکتر از 1 بود، چاپ کند جواب شما بی معنی است و اگر عدد بزرگتر از1 بود، محاسبه را انجام دهد

13 - برنامه ای بنویسید که عدد فردN را بخواند و سری زیر را با استفاده از حلقه for محاسبه نماید

\[s=1+\frac{1}{2!}+\frac{1}{3!}+...+\frac{1}{N!}\]

14 - با استفاده از ساختار switch-case برنامه ای بنویسید که مقدار دما رابر اساس واحدی که کاربر مشخص میکند، دریافت کند و آن را بر حسب واحد دیگری نمایش بدهد

\[\begin{matrix} K=C+273\\ F=1.8C+32\\ R=1.8C+491.4 \end{matrix}\]

15 - دستوری بنویسید که چندجمله ای زیر را در متلب نمایش دهد.مقدار چند جمله ای فوق را در نقطهx=1 بیابید.

\[f(x)=3x^{4}-0.5x^{3}+x-5.2\]

16 - دو چند جمله ای زیر را در هم ضرب کرده و چند جمله ای حاصل را بنویسید.خارج قسمت و باقی مانده تقسیم تابعg(x)برf(x)رانیز حساب کنید

\[\begin{matrix} f(x)=3x^{3}-5x^{2}+6x+2 \\ g(x)=x^{5}+3x^{4}-x^{2}+2.5 \end{matrix}\]

17 - نمودار دو چند جمله ای زیر را در یک پنجره شکل رسم کنید

\[\begin{matrix} f(x)=3x^{4}+2x^{3}+7x^{2}+2x+20 \\ g(x)=5x^{3}+9x-2 \end{matrix}\]

18 - ریشه های چند جمله ای زیر را بیابید

\[F=x^3+3x+1\]

19 - تابع بهترین چند جمله ای درجه 3 و درجه 4 عبوری از نقاط زیر را به دست آورید و نمودار تابع را رسم کنید.

A=[1 2 3 7;6 7 22 32;98 5 -23 1;32 5 -75 23]

20 - دستگاه معادلات خطی زیر را حل کنید.

\[\left\{\begin{matrix} x+2y+3z+7t=4\\ 6x+7y+22z+32t=5\\ 98x+5y-23z+t=7\\ 32x+5y-75z+23t=1 \end{matrix}\right.\]

21 - برنامه ای بنویسید که ماتریس ضرایب و مقادیر سمت راست یک دستگاه معادلات خطی را از کاربر بگیرد و پاسخ دستگاه را با پیغام مناسب نمایش دهد.

22 - تابعی در متلب MATLAB  بنویسید که یک آرایه خطی از کاربر دریافت ، کوچکترین و بزرگترین مقادیر را حذف و اگر پس از آن مقادیر تکراری در صورت وجود را حذف و در نهایت آرایه تغییر یافته را چاپ کند.

23 - با استفاده از روش نیوتن - رافسون و گاوس سایدل ( هر دو روش ) پاسخ یکی از معادلات زیر را حداقل تا شش رقم اعشار بیابید. برای این کار هر مرحله را درون یک حلقه ی تکرار قرار دهیدو نتایج بدست آمده در هر مرحله را در یک ماتریس ذخیره کنید. پس از حلقه تکرار ، کل ماتریس نتایح را در یک فایل اکسل بنویسید، نمودار را نیر ترسیم نمایید. در انتها نتایج هر دو روش را با هم مقایسه نماید و از دستور شرطی برای نمایش نتیجه استفاده نمایید.

\[f(x)=sin(x)-x \;\;\;\;\;\;\; x\in \left [ 0 , 2 \right ]\]

\[f(x)=e^{x}-x \;\;\;\;\;\;\; x_{0}=0\]

\[f(x)=x^{5}-1 \;\;\;\;\;\;\; x_{0}=0.5\]

24 - برنامه ای بنویسید که حاصل عبارت زیر را محاسبه کند.

\[\prod_{j=1}^{100} \frac{j-3}{j-8}\]

25 - برنامه ای بنویسید که N را از ورودی دریافت کند و یک جدول ضرب N*N را تولید و چاپ کند. همچنین فلوچارت آن را نیز رسم کنید.

26 - برنامه ای بنویسید که تابع های زیر را در بازه های خواسته شده رسم کند.

\[f(x)=e^{ \frac{-1}{2} x}cos(4x)\]

\[f(x)=\begin{cases} sin(x)& \text{ if } x\in [-2\pi,2\pi] \\ x^{2}-1& \text{ if } x\in[2\pi,10] \\ 4& \text{ if } x\in otherwise \end{cases}\]

27 - برنامه ای بنویسید که N را از ورودی دریافت کرده و جدول زیر را چاپ کند.

\[\begin{bmatrix}1 & 2 & 3 &... &N \\2 & 3 & 4 & ... & N+1 \\ 3& 4 & 5 & ... & N+2 \\ ...&... & ...& ... & ... \\ N& N+1 & N+2 & ... & 2N+1 \\\end{bmatrix}\]

28 - برنامه ای بنویسید که نمودار تابع زیر در یک شکل شکل به طور همزمان ترسیم کند. در بازه 4 تا 4-

از دستور legend ، برچسب محورهای مختصات ، عنوان ، توضیحات برای هر نمودار وارد شود.

\[f(x)=\frac{1}{1+x^{2}} \;\;\; f(x)=sin(2x)\;\;\; f(x)=1-cos(x)\]

29 - با استفاده از روش رامبرگ  انتگرال تابع دلخواهی را در بازه مشخص شده محاسبه کنید.

30 - تابعی بنویسید که بزرگترین مقسوم علیه مشترک را محاسبه کند.

31 - برنامه ای بنویسید که تا زمانی که دو آرایه دو بعدی ( ماتریس ) با ابعاد برابر وارد نکنیم از کاربر بخواهد دوباره ماتریسی را وارد نماید.

32 - تابعی بنویسید که فاصله اقلیدسی بین دو بردار را بدست آورد. بردارها ورودی تابع هستند که می توانند به صورت سطری یا ستونی باشند.

33 - یک جمله ای با بیش از 10 کلمه را به صورت ورودی دریافت کنید و برنامه ای بنویسید که تعداد کلمات این جمله را مشخص نماید و حروف کوچک درون جمله را به حروف بزرگ تبدیل کند.

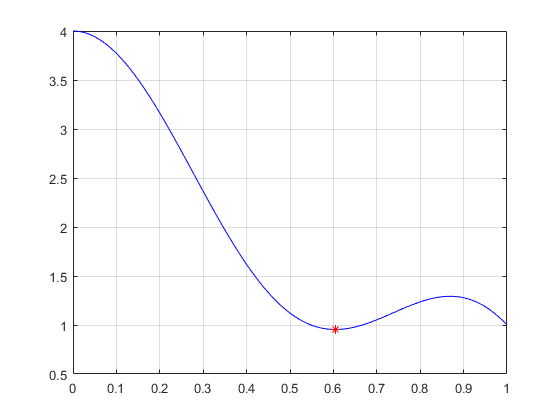
34 - مینیمم min محلی یک سیگنال سینوسی زیر را در بازه  0 تا 1 بدست آورید و منحنی آن را نیز رسم کنید.

\[y(t)=cos(2\pi t)+3cos(\frac{1}{2} \pi t)\]

35 - در بازی گوسین عددی صحیح بین 1 تا 10 به صورت تصادفی انتخاب می شود. در صورتی که حدس شما از این عدد بزرگتر باشد ، جمله Too High و در صورتی که حدس شما از این عدد کوچکتر باشد جمله Too Low را نمایش دهد. این بازی تا زمانی ادامه دارد که کاربر عدد مورد نظر را وارد نماید. برنامه این بازی را بنویسید.

36 - با استفاده از دستور fsolve معادلات غیرخطی زیر را حل کنید.

\[ \left\{\begin{matrix} x_{1}^{2}+4x_{2}^{2}=5\\2x_{1}^{2}-2x_{1}-3x_{2}=2.5\end{matrix}\right. \;\;\;\;\; x_{1,0}=0.8 \;\;,\;\; x_{2,0}=0.2\]

37 - نمودار تابع زیر را با دستور semilogy در بازه [0,30]  رسم کنید. محورهای مختصات را نام گذاری کنید و نمودار را شبکه بندی نمایید.

\[ y(t)=\frac{2+sin(t)}{2-cos(\frac{t}{4})}e^{-0.05t}\]

38 - نمودار تابع غیرخطی را رسم نمایید.

\[ y(t)=\left| \frac{sin(50t)}{t} \right|sin(t+\pi)\]

سپس نمودار را hold کرده و تابع زیر را نیز رسم کنید.

\[ f(z)=10e^{z}\;\;\;\; z \in[0.01+0.5i,-1+50i]\]

39 -معادله یک بیضی در سیستم مختصات قطبی به صورت زیر است. نمودار r بر حسب theta را رسم کنید.

\[r=\frac{a(1-b^{2})}{1-bcos(\theta)}\;\;\;\;\; a=2\;,\;b=0.5\]

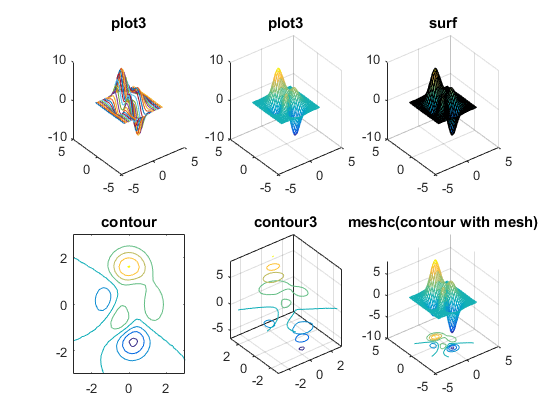
40 - نمودار منحنی زیر را با دستور surf رسم نمایید.

\[f(x,y)=cos(x)cos(y)\]

41 - نمودار منحنی پارامتری را بر حسب توابع زیر در بازه خواسته شده رسم کنید. ( plot3 )

\[\left\{\begin{matrix} x(t)=sin(2t)+sin(t)^2\\ y(t)=t\\z(t)=cos(2t)+cos(t)^2\end{matrix}\right. \;\;\;\;\;\;\; t \in [0,10\pi]\]

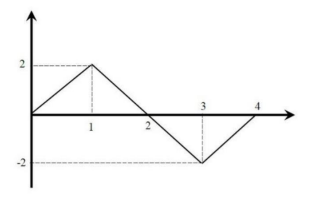
42 - تابع گسسته زیر را رسم کنید

\[y[n]=25cos(\pi n+5)e^{0.1n}\;\;\;\;\;n=0,1,2,...,40\]

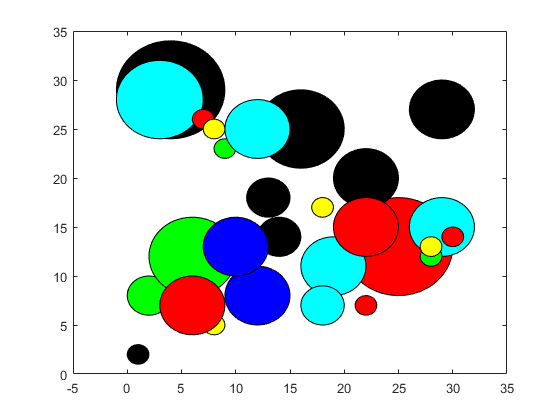
43 - یک تابعی بنویسید که یک دایره را رسم نماید به طوری که آرگومان های ورودی آن (x,y,r) باشد که x و y مختصات مرکز دایره و r شعاع دایره است. برای استفاده و اجرای تابع مذکور 30 بار آن را اجرا نمایید که دایره ها شعاع و مرکز تصادفی داشته باشند و همه 30 دایره را در یک پنجره رسم نمایید.

44 - حاصل ضرب تابع چند جمله ای زیر را محاسبه کنید.

\[(x^{2}-x-1)(x^{3}-2)(x^{2}-3)\]

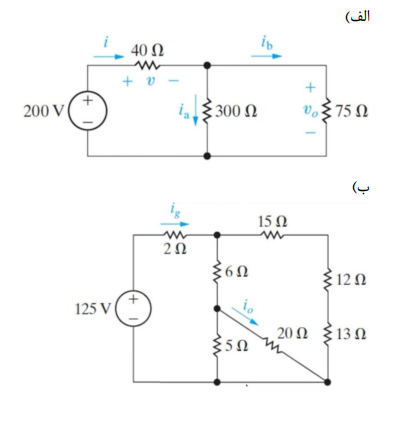
45 - با اعمال قوانین کیرشف ، دستگاه معادلات خطی زیر را برای یک نمونه مدار بدست آورید و مقادیر جریان ها را محاسبه کنید.

\[\left\{\begin{matrix} 470i_{1}+300i_{2}-5=0\\ -300i_{2}+560i_{3}+1000i_{5}=0\\ 100i_{4}-560i_{3}+10=0\\ -i_{1}+i_{2}+i_{3}+i_{4}=0\\-i_{4}-i_{3}+i_{5}=0\end{matrix}\right.\]

46 - مقدار انتگرال زیر را محاسبه کنید.

\[\int_{-2}^{6} \frac{5}{4}x^{6}-2x^{5}+0.2x^{3}-7\;\;\;\;dx\]

47 - برنامه ای بنویسید که شماره دانشجویی و معدل دانشجویان یک کلاس ٢٠ نفری را دریافت کرده و معدل و شماره دانشجویی سه شاگرد برتر را برگرداند.

48 - برنامه ای بنویسید که یک بردار از اعداد صحیح مثبت با طول دلخواه دریافت کند و عناصر تکراری آن ماتریس را حذف کند

49 - برنامه ای بنویسید که یک بردار دلخواه را از کاربر دریافت کند. به جای درایه های زوج مثبت آن منفی آن ها و به جای درایه های فرد مثبت آن ١ −قرار دهد. به جای درایه های زوج منفی آن توان دوم آن ها و به جای درایه های فرد منفی آن ها منفی دوبرابر آن ها را قرار دهد. در انتها درایه های بردار را به صورت زیر مرتب کند.

درایه های مثبت از کوچک به بزرگ,درایه های منفی از بزرگ به کوچͷ,درایه های صفر

50 -

| جهت سفارش پروژه ، تکلیف و آموزش نرم افزار متلب MATLAB  لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.

1 - الف) ماتریس زیر را ایجاد کنید. (از نوشتن اعضای ماتریس به صورت تک تک خودداری کنید)

ب ) یک ماتریس 10 * 10 ایجاد کنید که درایه های روی قطر اصلی آن pi ، یک ردیف بالای قطر اصلی e  و یک ردیف زیر قطر اصلی آن  i باشد.

2 - برنامه ای بنویسد که یک ماتریس دلخواه را از کاربر دریافت کرده و سپس اطلاعات زیر را چاپ کند:

الف) تعداد سطر وستون ماتریس

ب) بیشترین و کمترین عنصر

ج) ماتریس معکوس پذیر است یا خیر؟

د) مقدار ویژه آن را از بزرگ به کوچک نمایش دهد .

3 - برنامه ای بنویسید که مختصات چهار نقطه را در فضا دریافت کند و سپس بررسی کند آیا این چهار نقطه در یک صفحه قرار دارند؟ درصورتی که داخل یک صفحه باشند کلمه yes درغیر اینصورت کلمه no را چاپ کند. ضمنا بارسم شکل مناسب صحت این ادعا را نمایش دهد. با ذکر مثال درستی برنامه را نمایش دهید.

4 - برنامه ای بنویسید که دو بردار را از کاربر دریافت کند اب تدا دو بردار عمود بر آن دو بردار را محاسب ه و در پنجره فرمان نمایش دهد سپس هر چهار بردار را در صفحه رسم نماید. با ذکر مثال درستی برنامه را نمایش دهید.

5 - تغییراتی در تابع arrow ایجاد کنید که ضخامت مربوط به بردار را از کاربر دریافت کرده و با ضخامت دلخواه کاربر رسم کند .

6 - برنامه ای بنویسید که معادله دو خط را در صفحه دریافت کند سپس
الف) در صورت متقاطع بودن زاویه بین دو خط را محاسبه و در پنجره فرمان نمایش دهد.
ب) در صورت متوازی بودن دو خط فاصله آن ها را از یکدیگر چاپ کند.

7 - سطح peaks(30) با چندین دستور رسم شده است. آن ها را با یکدیگر مقایسه کنید. توابع مربوط به هریک را بنویسید.

8 - تابعی بنویسید که یک چند جمله ای ( به صورت یک بردار سطری ) و یک بردار دو عنصری ( حاوی دامنه ترسیم ) را از کاربر بگیرد و نمودار چندجمله ای را در دامنه مشخص شده ترسیم کند.

9 - تابع سوال قبل را طوری تغییر دهید که اگر با دو آرگومان خروجی به کاربرده شود به جای ترسیم ، مقادیر x و y محاسبه شده را بازگرداند.

10 - تابع y=exp(x) را در دامنه 2- تا 2 در گام های 0.1 رسم کنید. نمودار دارای عنوان مناسب و محورها دارای برچسب باشد.

11 - نمودار تابع y=sin(x) را در بازه 0 تا pi در دو نمودا رجداگانه یک بار با 10 نقطه در این بازه و یک بار با 100 نقطه در این بازه رسم کنید.

12 - یک فایل houseafford.dat در سه سال متوالی متوسط درآمد و میانگین قیمت خانه را به صورت یک ماتریس ذخیره می کند. مقدارها به صورت هر دلار 1000 دلار در نظر گرفته می شود. فرض کنید داده ها به صورت زیر باشد.

2007	2006	2005	2004	2003	2002	2001	200
93	89	83	80	77	74	74	72
380	410	390	350	310	300	270	250

یک فایل در این فرمت ایجاد کنید و سپس ، نمودار میله ای آن را برای نشان دادن اطلاعات با عنوان مناسب بدست آورید.

13 - تابعی بنویسید که یک بردار ( آرایه سطری یا ستونی ) را از کاربر بگیرد و مراحل زیر را انجام دهد.

- تعداد آرگومان های ورودی و خروجی که توسط کاربر وارد شده است را چک کند و در صورتی که تعداد آرگومان ورودی بیشتر یا کمتر از یک و تعداد آرگومان خروجی بیشتر از یک باشد ، پیام خطا داده و از تابع خارج شود.

- ابعاد آرگومان ورودی را چک کند و در صورتی که آرایه ای غیر سطری یا غیر ستونی ( یعنی در صورتی که به جای بردار ماتریس باشد ) با پیغام خطا از تابع خارج شود.

- عبارت زیر را روی مقادیر ورودی اعمال نموده و عنوان خروجی بازگرداند.

14 - تابعی بنویسید که یک عبارت ریاضی دلخواه از کاربر ( به صورت یک رشته کاراکتری ) به عنوان آرگومان اول و یک آرایه به عناون آرگومان دوم بگیرد  و

- بررسی کند که تعداد آرگومان ورودی دقیقا دو عدد باشد ( با استفاده ار از تابع narginchk )

- بررسی کند که تعداد آرگومان خروجی دقیقا یک عدد باشد ( با استفاده از تابع nargoutchk )

- بررسی کند که آرگومان اول حتما یک رشته کاراکتری باشد و آرگومان دوم حتما یک متغیر عددی ( از توابع isstr و isnumeric استفاده شود ).

- با استفاده از تابع eval عبارت ریاضی وارد شده توسط کاربر را بر روی تمامی عناصر ورودی اعمال نموده ، بازگرداند.

16 - اسکریپتی بنویسید که از کاربر یک کاراکتر دریافت کند، سپس فاصله ی  2pi- تا 2pi را به 50 قسمت مساوی تقسیم کند و در x قرار دهد. y هم برابر cos(x) باشد. در صورتی که کاراکتر وارد شده r بود نمودار x-y را با رنگ قرمز و علامت * رسم نماید و در  غیر این صورت با رنگ قرمز و علامت + رسم کند.

17 - برنامه ای بنویسید که یک عدد طبیعی کمتر از 100 را از کاربر بگیرد و مضارب آن را که بزرگتر از 0 و کوچکتر از 1000 هستند را به کاربر نمایش دهد.

18 - دنباله ی فیبوناچی دنباله ای است که از صفر و سپس 1 شروع شده و هر جمله مجموع دو جمله قبلی می باشد. برنامه ای بنویسید که 100 جمله زوج ابتدایی از این دنباله را نمایش دهد.

19 - برنامه ای بنویسید که از کاربر بخواهد تعداد  15 عدد نمره دانشجویان از 20 را در مثلا درس ریاضی به ترتیب وارد نماید. این نمرات باید در ماتریسی ذخیره شوند. سپس برنامه تعداد نمرات کمتر از 10 را به کاربر نمایش بدهد. سپس برنامه باید نمرات کمتر از 10 را از ماتریس حذف کند.

20 - تابعی بنویسید که یک عدد طبیعی را به عنوان ورودی دریافت کند ، سپس اعدا اول کمتر از آن عدد را به عنوان خروجی به کاربر نمایس دهد.

21 - با استفاده از دستور subplot چهار تابع cos(x) , sin(x) , log(x) , floor(x) را در یک صفحه 2*2 هر کدام در یک قسمت رسم نمایید. رنگ و مارکرهای رسم هر نمودار با دیگری تفاوت داشته باشد و همه نمودارها باید دارای عنوان باشند.

 

جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink  و  متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره  989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.