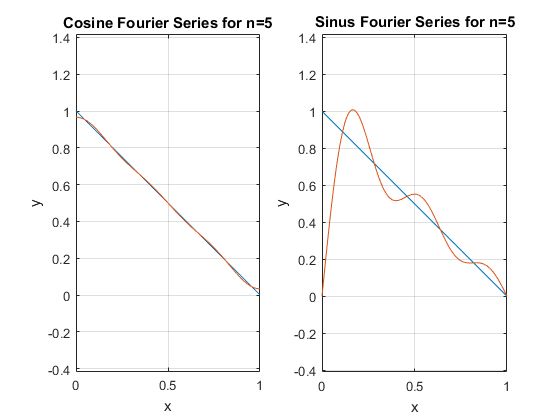
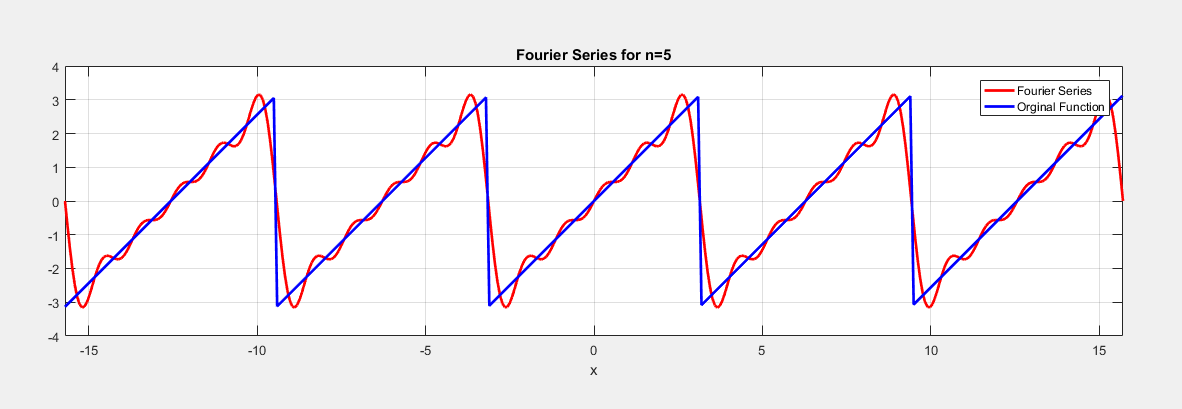
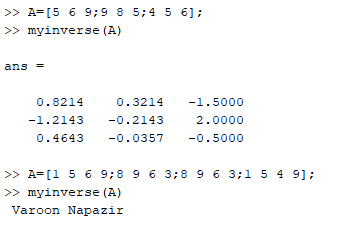
1 - در این پروژه قصد داریم وارون پذیری هر ماتریس را بدون استفاده ار توابع متلب ( محاسبه به صورت ریاضی ) را بررسی کرده و در صورت وجود مقدار آن را محاسبه کنیم. تابعی بنویسید که یک ماتریس با ابعاد دلخواه دریافت کند و مشخص کند که آیا وارون پذیر است یا خیر و وارون آن را نمایش دهد.
2 - برنامه ای بنویسید که به ازای هر عدد صحیح مثبت که از ورودی دریافت می کند ، خروجی مطابق شکل روبرو ایجاد کند. مثلا برای n=5 خروجی مقابل چاپ گردد.
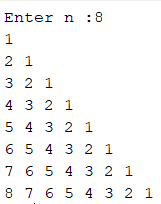
3 - برنامه ای بنویسید که به ازای هر عدد صحیح مثبت که از ورودی دریافت می کند ، خروجی مطابق شکل روبرو ایجاد کند. مثلا برای n=12 خروجی مقابل چاپ گردد.

4 - برنامه ای بنویسید که به ازای دریافت یک زاویه ( بر حسب درجه ) از ورودی ، سینوس آن زاویه را به وسیله رابط مقابل محاسبه کند. ( در رابطه مقابل زاویه بر حسب رادیان است ). عملیات محاسبه بایستی تا زمانی ادامه پیدا کند که اختلاف بین رابطه مقابل با مقدار تابع تعریف شده در متلب sin(x) کوچکتر از 0.0001 گردد. برنامه بایستی در نهایت مقدار سینوس بدست آمده از رابطه مقابل ، سینوس محاسبه شده با تابع sin(x) و مقدار n در رابطه روبرو را نمایش دهد. ( یعنی در چندمین جمله ، اختلاف کمتر از 0.0001 شده است )
\[sin(x)=\sum_{n=0}^{\infty }\frac{(-1)^n}{(2n+1)!}x^{2n+1}\]
5 - برنامه ای بنویسید که مقدار عدد pi را از رابطه روبرو به ازای مقادیر
\[\pi=4\sum_{n=1}^{\infty}(-1)^{(n-1)}(\frac{1}{2n-1})\]
الف ) n=20
ب ) n=50
محاسبه نماید. در هر حالت ، اختلاف عدد pi بدست آمده از رابطه مقابل را با تابع تعریف شده pi در متلب نمایش دهد.
6 - سری مقابل با عددهای 0 و 1 شروع می شود و باقی اعداد سری هر کدام از جمع دو عدد قبل خود به دست می آید. برنامه ای بنویسید که یک عدد صحیح را به عنوان n امین عضو سری از ورودی دریافت کرده و سپس سری مقابل را تا عضو مربوطه نمایش دهد.
7 - دستگاه زیر را به کمک ضرب ماتریسی در MATLAB حل کنید
\[\left\{\begin{matrix} 2x-y+3z=15\\ 5x-6y-z=10\\7x+8y-9z=11\end{matrix}\right.\]
ماتریس ضرایب فوق را در نظر بگیرید و جذر ماتریس A و جذر درایه های ماتریس A را چاپ کنید.
8 - برنامه ای بنویسید که تبدیل یک عدد اعشاری کوچکتر از یک ( عدد اعشاری ) را به مبنای r ( برای مبنای 2 امتحان کنید)
9 - برنامه ای بنویسید که شماره ی روز تولد یک نفر در سال را گرفته و روز و ماه تولد را تعیین کند.
10 - برنامه ای بنویسید که دو عدد صحیح و مثبت m و n را دریافت کرده و ب م م و ک م م آن ها را محاسبه و چاپ کند.
11 - تابعی به نام sumdg بنویسید که عدد طبیعیn را دریافت و تعداد ارقام و نیز مجموع آن ها را محاسبه و چاپ کند.
12 - تابعی به نام c2ten بنویسید که عددی در مبنای 2 را گرفته و معادل آن در مبنای 10 را بنویسد.
13 - تابعی به نام ctwo10 بنویسید که عددی را در مبنای 10 گرفته و معادل آن را در مبنای 2 بنویسد.
14 - برنامه ای بنویسید که 100 عدد را دریافت کند و آن هایی که مضرب 3 هستند به صورت نزولی ( از بزرگ به کوچک ) چاپ کند.
15 - ماتریسی 6 * 4 با درایه های تصادفی ایجاد نمایید و سپس سطرهای زوج این ماتریس را حذف نمایید؟
16 - برداری با 6 درایه از 1 تا 10 با فواصل مساوی تشکیل دهید؟
17 - ماتریسی 5 * 5 ایجاد نمایید که مجموع سطرها، ستون ها و قطر آن با هم برابر باشد؟ بزرگترین و کوچکترین درایه این ماتریس را به دست آورید؟ هم چنین درایه هایی از ماتریس را که اعداد اول هستند مشخص نمایید؟
18 - یک مخروط را در نظر بگیریم. یک برنامه Matlab بنویسید که حجم مخروط را محاسبه کند. در اینجا فرمولی است که باید از آن استفاده کنید.
\[V=\frac{1}{3}hr^{2}\]
جایی که r شعاع پایه و h ارتفاع است. یک برنامه Matlab بنویسید که حجم مخروط را پیدا کند. برنامه ابتدا باید بررسی کند که r و h هر دو مثبت هستند. دقت نتیجه باید حداکثر 3 رقم اعشاری باشد.
19 - یک برنامه متلب بنویسید که در هنگام درخواست مقدار x و n از کاربر ، مقدار زیر را محاسبه کند.
\[y=\sum_{k=1}^{n}\left ( \frac{2}{x} \right )^{k}\]
20 - معادله زیر را با استفاده از Matlab حل کنید.
\[\left\{\begin{matrix} x_{1}+3x_{2}=19\\ 4x_{1}+2x_{2}+5x_{3}=26\\7x_{2}-10x_{3}=35\end{matrix}\right.\]
21 - نمودار توابع زیر را در فاصله 0 تا 2pi که به 200 قسمت مساوی تقسیم شده ترسیم نمایید
\[exp(x) \;\;\;, \;\; sin(2x)+cos(2x)\;\;\; , \;\;tan(\sqrt {x}))\]
22 برنامه ای بنویسید که یک ماتریس 3 در 3 را از ورودی دریافت کند و مشخص نماید آیا ماتریس متقارن است یا خیر
23 - برنامه ای بنویسید که با گرفتن دو عدد x و y از کاربر ، مقدار تابع f را محاسبه نماید.
\[ f=\left\{\begin{matrix} xy+25&x>0\;\; and \;\; y>0 \\ x^{3}+y^{3}& x<0 \;\; or \;\; y<0\\\end{matrix}\right.\]
24 - برنامه ای بنویسید که تعداد سطر و ستون یک آرایه را از کاربر بگیرد و آرایه خروجی به صورت تصادفی بین 0 تا 9 نمایش دهد.
25 - یک کد محاسباتی بنویسید که یک تابع جدولی را که در یک فایل متنی ذخیره شده است، به عنوان ورودی دریافت کند. سپس اطلاعات آن را مرتب کرده و تشخیص دهد که آیا فاصله بین نقاط آن مساوی می باشد یا مساوی نمی باشد. سپس اگر فاصله نقاط مساوی نباشد، از کاربر سوال کند که از بین دو روش لاگرانژ یا روش تفاضلات تقسیم شده نیوتن از کدام روش برای به دست آوردن چند جمله ای میانیاب استفاده کند و اگر فاصله نقاط مساوی باشد، از کاربر سوال کند که از روش پیشرو نیوتن استفاده کند یا از روش پسرو! سپس جدول تفاضلات (به غیر از روش لاگرانژ) و چند جمله ای میانیاب را به عنوان جواب ارائه دهد. کد باید قابلیت این را داشته باشد که پس از به دست آوردن چند جمله ای میانیاب، مقدار تابع را در هر نقطه دلخواهی در بازه تابع جدولی محاسبه کند.
26 - پروژه های تخصصی درس نرم افزار ریاضی
دانشجویان علوم کامپیوتر از بین پروژه های زیر می توانند یک پروژه به دلخواه انتخاب کنند و با استفاده از متلب MATLAB پیاده سازی کنند.
- مسئله فروشنده دوره گرد
- مسئله n وزیر
- مسئله تعیین کوتاه ترین مسیر از مبدا
- مسئله تعیین یک درخت پوشای کمینه
- مرتب سازی سریع
- مرتب سازی ادغامی
- مرتب سازی حبابی
- مسئله همترازی دنباله ها DNA
- کدگذاری به روش هافمن
- مسئله کوله پشتی صفر و یک
دانشجویان ریاضیات و کاربردها از بین پروژه های زیر می توانند یک پروژه را به دلخواه انتخاب کنند.
- روش درون یابی لاگرانژ
- درون یابی نیوتن
- روش ژاکوبی
- روش نابجایی
- روش نیوتن رافسون
- روش نقطه ثابت
- روش وتری
- تقریب پیشرو و پسرو
- حل مساله بهینه سازی خطی در متلب
27 -
28 -
29 -
30 -
| جهت سفارش پروژه ، تکلیف و آموزش سیمولینک Simulink و متلب Matlab لطفا در شبکه های تلگرام و واتساپ موضوع و سوال مورد نظر را به شماره 989364847193+ ارسال نمایید، تا پس از بررسی هزینه خدمت شما اعلام گردد.